引用本文
叶克强, 黄明伟, 李君利, 唐劲天, 张建国. 125I放射性粒子在骨介质中剂量分布的蒙特卡罗模拟 . 北京大学学报(医学版), 2018,50(1): 131-135.
YE Ke-qiang, HUANG Ming-wei, LI Jun-li, TANG Jin-tian, ZHANG Jian-guo. Simulation of dose distribution in bone medium of 125I photon emitting source with Monte Carlo method . Journal of Peking University(Health Sciences), 2018,50(1): 131-135.  
Doi: 10.3969/j.issn.1671-167X.2018.01.022
Permissions
Copyright©2018, 北京大学
© 2010《北京大学学报（医学版）》编辑部
125I放射性粒子在骨介质中剂量分布的蒙特卡罗模拟
叶克强1, 黄明伟1,△, 李君利2, 唐劲天2, 张建国1
1. 北京大学口腔医学院·口腔医院, 口腔颌面外科 口腔数字化医疗技术和材料国家工程实验室 口腔数字医学北京市重点实验室, 北京 100081;
2. 清华大学工程物理系,粒子技术与辐射成像教育部重点实验室,高能辐射成像重点学科实验室, 北京 100084
收稿日期: 2017-10-10
基金资助: 国家自然科学基金(81502652)资助
摘要

目的 应用蒙特卡罗方法建立6711型125I放射性粒子模型,计算其在不同骨介质中的剂量分布,为进一步分析125I放射性粒子治疗头颈部肿瘤的剂量分布提供依据。方法 应用MCNP4C软件(截面库DLC-200)建立6711型125I放射性粒子模型,计算其剂量率常数及在水介质中的径向剂量函数值,并与美国医学物理学家协会(American Association of Physicists in Medicine,AAPM)2004年发布的TG43UI报告推荐值对比验证125I模型。利用该模型,采用ICRU44报告推荐的成人不同骨介质的元素组成及密度编写MCNP材料卡,计算125I模型在不同骨介质中的剂量分布。结果 应用MCNP4C软件建立的125I放射性粒子模型的几何形态及规格符合AAPM的TG43UI要求。模拟得到了125I模型剂量率常数Λ=0.977 78 cGy/(h·U)及在水介质中的径向剂量函数值,并得出125I模型在不同骨介质中的径向剂量分布。在同样的介质深度,125I粒子的剂量沉积能力自骨皮质、骨松质、软骨、水、黄骨髓、红骨髓依次递减。在介质深度分别为0.01、0.1、1 cm处,125I粒子在骨皮质中的剂量沉积分别是在水中的12.90倍、9.72倍、0.30倍。结论 本研究建立的125I放射性粒子模型可靠性好,可用于后续在骨介质中的模拟计算。125I放射性粒子在不同的骨介质中的剂量分布不等同于水,能量主要沉积在骨介质表面,因此在制定靶区毗邻骨组织的125I粒子植入计划时应考虑骨介质的影响。

关键词: 蒙特卡罗法; 碘放射性同位素:骨; 辐射剂量; 近距离放射疗法
中图分类号:R730.55 文献标志码:A 文章编号:1671-167X(2018)01-0131-05
Simulation of dose distribution in bone medium of 125I photon emitting source with Monte Carlo method
YE Ke-qiang1, HUANG Ming-wei1,△, LI Jun-li2, TANG Jin-tian2, ZHANG Jian-guo1
1. Department of Oral and Maxillofacial Surgery, Peking University School and Hospital of Stomatology & National Engineering Laboratory for Digital and Material Technology of Stomatology & Beijing Key Laboratory of Digital Stomatology, Beijing 100081, China;
2. Department of Engineering Physics, Tsinghua University, Key Laboratory of Particle and Radiation Imaging, Ministry of Education, Key Laboratory of High Energy Radiation Imaging Fundamental Science,Beijing 100084, China
△ Corresponding author’s e-mail, hmwd97@126.com
Fund:Supported by the National Natural Science Foundation of China (81502652)
Abstract

Objective: To present a theoretical analysis of how the presence of bone in interstitial brachytherapy affects dose rate distributions with MCNP4C Monte Carlo code and to prepare for the next clinical study on the dose distribution of interstitial brachytherapy in head and neck neoplasm.Methods: Type 6711,125I brachytherapy source was simulated with MCNP4C Monte Carlo code whose cross section library was DLC-200. The dose distribution along the transverse axis in water and dose constant were compared with the American Association of Physicists in Medicine (AAPM) TG43UI update dosimetry formalism and current literature. The validated computer code was then applied to simple homogeneous bone tissue model to determine the affected different bone tissue had on dose distribution from125I interstitial implant.Results:125I brachytherapy source simulated with MCNP4C Monte Carlo code met the requirements of TG43UI report. Dose rate constant, 0.977 78 cGy/(h·U), was in agreement within 1.32% compared with the recommended value of TG43UI. There was a good agreement between TG43UI about the dosimetric parameters at distances of 1 to 10 cm along the transverse axis of the125I source established by MCNP4C and current published data. And the dose distribution of125I photon emitting source in different bone tissue was calculated. Dose-deposition capacity of photons was in decreasing order: cortical bone, spongy bone, cartilage, yellow bone marrow, red bone marrow in the same medium depth. Photons deposited significantly in traversal axis among the phantom material of cortical bone and sponge bone relevant to the dose to water. In the medium depth of 0.01 cm, 0.1 cm, and 1 cm, the dose in the cortical bone was 12.90 times, 9.72 times, and 0.30 times of water respectively.Conclusion: This study build a125I source model with MCNP4C Monte Carlo code, which is validated, and could be used in subsequent study. Dose distribution of photons in different bone medium is not the same as water, and its main energy deposits in bone medium surface, so we should consider the effect of bone medium when we design the target area adjacent to the bone tissue in125I sources implantation plan.

Key words: Monte Carlo method; Iodine radioisotopes; Bone; Radiation dosage; Brachytherapy

组织间植入放射性粒子近距离治疗肿瘤具有局部控制率高、微创、高度适形及毒副反应小等优势[1], 在前列腺、头颈部、肺、肝、胰腺等部位的实体肿瘤治疗中已取得良好的临床疗效[2, 3]。

目前, 在临床上进行的剂量计算中, 均是把人体组织模拟为水模体, 但与软组织相比较, 光子在骨介质中的剂量沉积与水介质有明显差异[4], 125I放射性粒子所释放的γ 射线即为光子。在前列腺、肺、肝等部位的肿瘤治疗中, 由于靶区均为软组织, 且距离骨组织较远, 所以骨组织对其剂量分布的影响较小, 而当125I放射性粒子治疗头颈部肿瘤时, 靶区内常存在或毗邻大量骨组织, 因此在制定治疗计划、设计处方剂量、疗效评估时, 明确125I放射性粒子在骨组织内剂量分布的影响对进一步提高疗效、同时降低毒副反应有着重要意义。

蒙特卡罗(Monte Carlo)模拟也称统计试验方法, 是一种基于概率论解决物理和数学问题的统计学方法, 可有效处理不同介质中的光子输运问题及不同组织中密度和原子序数的变化对于剂量沉积的影响, 其数值结果已经成为比较其他理论方法的非试验金标准[5, 6]。

本研究通过蒙特卡罗模拟方法建立125I粒子剂量场模型, 并利用该模型计算125I放射性粒子在人体骨介质(骨皮质、骨松质、黄骨髓、红骨髓以及软骨)中的剂量分布情况, 为临床中对邻近骨组织的靶区进行125I放射性粒子布源及剂量计算提供参考依据。

1 材料与方法
1.1 剂量计算相关参数及公式

美国医学物理学家协会(American Association of Physicists in Medicine, AAPM)于1995年发布了指导近距离治疗剂量计算的TG-43报告, 随着近距离治疗的不断发展, 于2004年发布了其修订版TG43UI, 2007年再次对其进行了补充。

本研究的剂量计算所用公式[7]如下:

Λ=D·(r0, θ0)SK(1)

g(r)=D·r, π2Gr, π2D·(r0, θ0)G(r0, θ0)(2)

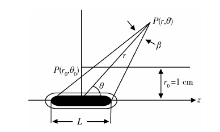
公式(1)和(2)所用的极坐标系统如图1。在极坐标系统下, Λ 为剂量率常数, 指的是参考点处的剂量率, 单位cGy/(h· U)。 D·为吸收剂量。Sk为空气比释动能强度(air-kerma strength), 专用符号为U, 1 U=1 μ Gym2/h=1 cGycm2/h。r为从放射性粒子中心处至关心点的距离(cm), 参考距离r0为距离放射性粒子长轴1 cm的距离。θ 为放射性粒子中心与关心点的连线与放射性粒子长轴方向的夹角, 参考角度θ 0为与放射性粒子长轴方向夹角成90° 或π /2弧度。g(r)为径向剂量函数, G(r, θ )为几何函数。L为线性放射源近似的功能长度(cm)。P(r0, θ 0)为距离放射性粒子长轴r0的距离和与放射性粒子长轴方向夹角成θ 0的参考点, P(r, θ )为放射性粒子中心距离关心点距离为r、夹角为θ 的点。β 为放射性粒子的功能长度与P(r, θ )所形成的三角形中, 放射性粒子功能长度的对角, 以上各个参数的详细说明及计算方法见TG43UI[7]。

图1 剂量计算所使用的极坐标系统Figure 1 Coordinate system used for brachytherapy dosimetry calculations

1.2 建立125I粒子源蒙特卡罗模型

模拟粒子源为125I放射性粒子(6711型, 宁波君安药业科技有限公司), 半衰期为59.40 d, 发射的光子能量分别为27.202、27.472、30.980、31.710、35.492 keV, 对应的每次衰变发出的光子数分别为0.406 0、0.757 0、0.202 0、0.043 9、0.066 8。采用蒙特卡罗MCNP4C程序, 在极坐标系统下, 建立125I放射性粒子蒙特卡罗模型。放射性粒子中介质的物理参数如表1所示。

表1 125I放射性粒子中相关介质的物理参数 Table 1 Physical parameters of the mediums about 125I photon emitting source
1.3 剂量率常数Λ 的计算

依据公式(1), 在垂直于粒子源中心轴方向1 cm处取两个体积为0.04 cm3的栅元, 一个用于填充空气材料, 另一个填充水材料, 使用* F4卡和质量能量吸收系数计算沉积在两个栅元中的剂量, 两者的比值即为剂量率常数[8]。

1.4 水介质中径向剂量的验证

将125I放射性粒子源置于半径为30 cm的液态水球中心, 在源中垂轴的正、负方向上各布置1组计算点, 每组包含16个计算点, 分别距源中心0.10、0.15、0.25、0.50、0.75、1.00、1.50、2.00、3.00、4.00、5.00、6.00、7.00、8.00、9.00和10.00 cm。计算上述这些位置上的吸收剂量, 将正、负方向上距离相同两点处的数值进行平均后作为该距离处的吸收剂量值。依据公式(2)求得各距离上径向剂量函数值, 单次计算时间为250~550 min, 模拟的光子数为108~109个, 将所得结果与TG43UI推荐数值及部分国内已发表的数据进行比较, 以验证本次模拟建模的可靠性。

1.5 有界骨介质中125I剂量场模拟

建立单一125I粒子源对不同骨介质的照射模型。以半径为30 cm建立真空球形模型, 125I放射性粒子置于模型中心, γ 射线产生的光子在真空运行中不发生衰减和吸收, 直至撞击骨面。骨组织规格:5 cm× 5 cm× 4 cm (厚), 距粒子源1 cm。取较大边界条件, 保证光子在传输过程中基本不会逃逸出组织, 得到光子沿不同厚度骨介质的能量密度分布。光子入射骨组织后随机发生吸收和散射反应, 直到能量被吸收低于阈值或溢出组织。记录每个光子被吸收的能量和位置, 大量光子在组织中随机反应的统计结果就形成有界骨组织中的剂量分布。采用ICRU44报告推荐的成人骨皮质、骨松质、黄骨髓、红骨髓以及软骨的元素及密度组成[9](表2), 以同样的模型, 将骨组织的材料卡转为水介质的材料卡进行计算, 比较光子在骨组织和液态水中剂量分布的差异。模拟光子数为108~109个, 分析其在不同骨介质中的剂量分布。

表2 ICRU44报告推荐人体骨介质元素及密度组成* Table 2 Recommended mass and densities of the bone mediums from ICRU report 44*
2 结果

MCNP4C所建立的6711型125I放射性粒子模型如图2所示, 最外层为钛壳, 钛壳与内部的银棒以空气相隔, 125I核素分布在银棒表面。

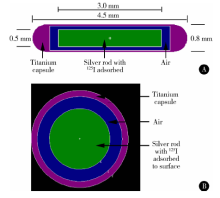图2 MCNP4C建立125I粒子模型平行长轴(A)及垂直长轴(B)截面图Figure 2 Sectional views of 125I source in MCNP4C (A, parallel to the long axis; B, perpendicular to the long axis)

模拟计算得到125I模型在水介质中的剂量率常数Λ =0.977 78 cGy/(h· U)。125I在水介质中的径向剂量函数计算值与TG43UI报告理论值[7]以及孙亮等[10]的报道值的对比结果见表3。

表3 本实验径向剂量计算值与TG43UI报告及其他研究的报道值对比 Table 3 Comparation of the g(r) values for 125I source in this study, TG43UI report, and other research

125I放射性粒子在不同骨介质和液态水中不同距离的单光子剂量沉积见图3, 反映了125I放射性粒子剂量场下γ 射线在不同介质中不同深度的能量沉积情况。图中横坐标为光子进入介质的深度, 纵坐标为相对剂量分布, 所有介质内探测单元统计性误差均控制在5%以内。结果表明, 在不同介质中, 125I粒子辐射场的能量分布存在明显差异。同样介质深度下, 光子的沉积能力自骨皮质、骨松质、软骨、水、黄骨髓、红骨髓依次递减。125I剂量场下, 光子在进入介质表面极浅表的位置时主要发生光电效应, 光子转化为电子在介质中迅速沉积, 随着进入介质深度的增加, 其能量沉积呈指数衰减趋势, 主要发生康普顿散射(Compton scattering)。

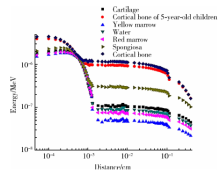图3 骨介质及水中125I剂量场能量沉积随深度变化规律Figure 3 Dose distribution in bone medium and water of single 125I source

骨介质与水介质在相同深度的剂量沉积差异较大, 在介质深度0.01 cm、0.1 cm、1 cm处, 125I粒子在骨皮质中的剂量沉积分别是在水中的12.90倍、9.72倍、0.30倍。由实验数据可推算出, 当单个活度为0.8 mCi的125I放射性粒子植入骨皮质或水中, 在距离125I放射性粒子为0.01 cm、0.1 cm、1 cm处时, 骨皮质所沉积的剂量为110.2 Gy、66.9 Gy、0.4 Gy, 水介质所沉积的剂量为16.4 Gy、13.2 Gy、2.8 Gy。

3 讨论

125I放射性粒子近距离治疗是治疗肿瘤的重要手段, 剂量的精确分布是其达到安全性和有效性的重要保障, 也是当前放射物理学面临的一个重要课题。临床上广泛应用的治疗计划系统(treatment planning system, TPS)将人体骨组织、软组织等效为液态水, 对不同组织间的介质差异未进行设计。在前列腺、肝、肺、胰腺等部位的近距离治疗中, 因靶区为软组织且毗邻骨组织较远, 其差异尚可接受, 但头颈部含有大量的骨组织, 相对肌肉、腺体等组织对电离辐射的吸收、散射的影响明显与水介质有区别[11, 12]。因此, 在对头颈部肿瘤靶区的术前设计中如何评估骨组织对剂量分布的影响, 进而优化术前设计, 是125I放射性粒子治疗头颈部肿瘤亟待解决的问题。

125I放射性粒子在骨介质中的剂量分布问题尚未见文献报道。由于人体解剖结构复杂, 个体差异大, 加之125I放射性粒子释放γ 射线能量较低, 仅为 27.202~35.492 keV, 采用热释光等剂量元件对125I粒子在骨介质中的能量沉积情况进行实验测定受到诸多限制, 故本实验选择蒙特卡罗模拟方法进行研究。

本研究中建立的125I放射性粒子蒙特卡罗模型, 其几何形态和规格符合TG43UI推荐值。模拟计算得出的剂量率常数与TG43UI推荐值[0.965 cGy/(h· U)]相差1.32%, 在水介质中的径向剂量函数数值非常接近TG43UI推荐值[7]及孙亮等[10]的研究结果(表3), 表明本研究所建立的125I放射性粒子蒙特卡罗模型可靠, 可用于后续研究125I粒子源在不同介质中的剂量分布。Belley等[4]的研究表明, 同等介质中, 光子源的平均能量决定了其在介质中的穿透和能量沉积能力, 不同组织介质中(骨、肌肉和水)光子的沉积能力存在明显差异, 且这种差异在光子能量为0.01~0.1 MeV的骨介质与水介质中明显[1], 并且可推测125I粒子在骨组织和水介质中剂量分布差异明显。本研究中125I粒子源在不同介质中剂量沉积的数据表明, 同样的介质深度, 125I放射性粒子所释放的γ 射线的沉积能力自骨皮质、骨松质、软骨、水、黄骨髓、红骨髓依次递减。125I放射性粒子能量沉积作用在骨介质表面处最为明显, 且骨皮质、骨松质的能量沉积迅速, 很快出现光子能量沉积的峰值, 随穿透深度增大, 与其他介质能量沉积的差异持续存在。临床治疗过程中, 随着植入粒子数量的增加, 这种差异的累积效应也将更明显。

本研究应用蒙特卡罗模拟建模的方式, 建立的125I放射性粒子模型较为精确地模拟了125I粒子源在水介质中的径向剂量分布, 模型可靠性好, 可用于后续其他组织的模拟计算; 采用不同的元素组成和密度模拟不同的介质, 得到实验难以测量的125I放射性粒子在骨介质中的剂量分布结果; 初步分析了125I放射性粒子在骨介质及水介质中剂量分布的差异, 可帮助临床医生对涉及骨组织靶区的术前设计进行优化; 同时, 本研究建立的模型及得到的相关剂量参数, 为后续研究125I放射性粒子治疗不同部位肿瘤的剂量分布提供了基础。

本研究在进行骨介质计算时, 其元素组成及密度采用ICRU44报告推荐值, 且为均质性模型, 而在临床应用中, 不同部位骨的厚度、组成不同, 多为多种骨介质混杂, 且元素分布、密度分布并不均匀。因此, 125I放射性粒子在人体的不同部位骨组织内的剂量分布还需要进一步研究。随着近距离治疗的不断发展, 对剂量计算的精度要求越来越高, 125I放射性粒子在骨介质中剂量分布的研究发展前景广阔。

(志谢:感谢北京大学口腔医院颌面外科的范祎老师对本研究的大力支持, 使研究得以顺利开展, 特此致谢!)

The authors have declared that no competing interests exist.

参考文献
[1] Davis BJ, Horwitz EM, Lee WR, et al. American Brachytherapy Society consensus guidelines for transrectal ultrasound-guided permanent prostate brachytherapy[J]. Brachytherapy, 2012, 11(1): 6-19. [本文引用:2]
[2] Huang MW, Zheng L, Liu SM, et al. 125I brachytherapy alone for recurrent or locally advanced adenoid cystic carcinoma of the oral and maxillofacial region[J]. Strahlenther Onkol, 2013, 189(6): 502-507. [本文引用:1]
[3] 张建国, 张杰, 宋铁砾, 等. 放射性粒子组织间植入治疗口腔颌面部恶性肿瘤初探[J]. 中华口腔医学杂志, 2006, 41(8): 464-466. [本文引用:1]
[4] Belley MD, Ashcraft KA, Lee CT, et al. Microdosimetric and biological effects of photon irradiation at different energies in bone marrow[J]. Radiat Res, 2015, 184(4): 378-391. [本文引用:2]
[5] Fill UA, Zankl M, Petoussi-Henss N, et al. Adult female voxel models of different stature and photon conversion coefficients for radiation protection[J]. Health Phys, 2004, 86(3): 253-272. [本文引用:1]
[6] Love PA, Lewis DG, Al-Affan IA, et al. Comparison of EGS4 and MCNP Monte Carlo codes when calculating radiotherapy depth doses[J]. Phys Med Biol, 1998, 43(5): 1351-1357. [本文引用:1]
[7] Rivard MJ, Coursey BM, DeWerd LA, et al. Update of AAPM Task Group No. 43 report: A revised AAPM protocol for brachytherapy dose calculations[J]. Med Phys, 2004, 31(3): 633. [本文引用:4]
[8] 王建华. 新型粒子源近距离治疗肿瘤剂量的蒙特卡罗模拟[D]. 湖南: 南华大学, 2006. [本文引用:1]
[9] Goldstone KE. ICRU: Tissue substitutes in radiation dosimetry and measurements. ICRU 1989 report 44, International Commission on Radiation Units and Measurements[J]. Clin Radiol, 1990, 41(3): 220. [本文引用:1]
[10] 孙亮, 李君利. 125I短程治疗源剂量计算参数的蒙特卡罗确定[J]. 原子能科学技术, 2006, 40(6): 657-661. [本文引用:2]
[11] Johnson JC, Langhorst SM, Loyalka SK, et al. Calculation of radiation dose at a bone-to-marrow interface using Monte Carlo modeling techniques (EGS4)[J]. J Nucl Med, 1992, 33(4): 623-628. [本文引用:1]
[12] Lee C, Lee C, Shah AP, et al. An assessment of bone marrow and bone endosteum dosimetry methods for photon sources[J]. Phys Med Biol, 2006, 51(21): 5391-5407. [本文引用:1]