引用本文
吴灵, 刘筱菁, 李自力, 王兴. 磨牙非中性关系与虚拟环境下拼对终末咬合精度. 北京大学学报(医学版), 2018,50(1): 154-159.
WU Ling, LIU Xiao-jing, LI Zi-li, WANG Xing. Evaluation of accuracy of virtual occlusal definition in Angle class Ⅰ molar relationship. Journal of Peking University(Health Sciences), 2018,50(1): 154-159.  
Doi: 10.3969/j.issn.1671-167X.2018.01.026
Permissions
Copyright©2018, 北京大学
© 2010《北京大学学报（医学版）》编辑部
磨牙非中性关系与虚拟环境下拼对终末咬合精度
吴灵, 刘筱菁, 李自力△, 王兴
北京大学口腔医学院·口腔医院,口腔颌面外科 口腔数字化医疗技术和材料国家工程实验室 口腔数字医学北京市重点实验室, 北京 100081
收稿日期: 2016-10-10
基金资助: 国家自然科学基金(81400569)、首都卫生发展科研专项(2016-1-4103)和北京市科学技术计划项目(Z161100000116053)资助
摘要

目的 检测磨牙非中性关系时虚拟咬合拼对的精度及临床可行性。方法 选取已完成正颌术前正畸、拼对终末咬合关系良好的寄存正颌患者牙列模型20副,其中10副术前正畸时上颌拔除左右各一颗双尖牙,术后拼对咬合为磨牙非中性关系(拔牙组), 另10副未进行减数拔牙,术后拼对咬合为中性磨牙关系(非拔牙组)。手工拼对石膏模型确立的终末咬合关系作为评价拔牙组、非拔牙组误差的实测值。进行虚拟终末咬合关系确立的数字流程为:结构光扫描仪分别获取上下牙列的三维数据,导入 3Shape软件,在虚拟环境下整体移动上颌牙列确立终末咬合关系。得到的测试上颌模型和手工拼对上颌模型以下颌模型为标准图形配准,采用直线距离法分析上颌牙列每颗牙齿的实验位置与手工拼对位置的差异,计算误差值。结果 拔牙组虚拟咬合拼对的全牙列平均误差为(0.60±0.36) mm,大于非拔牙组的(0.51±0.18) mm,差异有统计学意义( P<0.05);拔牙组误差与1 mm相比差异无统计学意义( P>0.05),非拔牙组误差小于1 mm,差异有统计学意义( P<0.05)。结论 磨牙非中性关系虚拟咬合拼对的误差值高于磨牙中性关系虚拟咬合拼对的误差值,但其精度满足临床需求,具备应用价值。

关键词: 计算机辅助手术模拟; 正颌外科; 虚拟终末咬合; 中性磨牙关系
中图分类号:R782.2 文献标志码:A 文章编号:1671-167X(2018)01-0154-06
Evaluation of accuracy of virtual occlusal definition in Angle class Ⅰ molar relationship
WU Ling, LIU Xiao-jing, LI Zi-li△, WANG Xing
Department of Maxillofacial Surgery, Peking University School and Hospital of Stomatology & National Engineering Laboratory for Digital and Material Technology of Stomatology & Beijing Key Laboratory of Digital Stomatology, Beijing 100081, China
△ Corresponding author’s e-mail, kglzl@sina.com
Fund:Supported by the National Natural Science Foundation of China (81400569), the Capital Health Researth and Development of Special (2016-1-4103) and Beijing Municipal Science & Technology Commission (Z161100000116053)
Abstract

Objective: To evaluate the accuracy of virtual occlusal definition in non-Angle class Ⅰ molar relationship, and to evaluate the clinical feasibility.Methods: Twenty pairs of models of orthognathic patients were included in this study. The inclusion criteria were: (1) finished with pre-surgical orthodontic treatment and (2) stable final occlusion. The exclusion criteria were: (1) existence of distorted teeth, (2) needs for segmentation, (3) defect of dentition except for orthodontic extraction ones, and (4) existence of tooth space. The tooth-extracted test group included 10 models with two premolars extracted during preoperative orthodontic treatment. Their molar relationships were not Angle class Ⅰ relationship. The non-tooth-extracted test group included another 10 models without teeth extracted, therefore their molar relationships were Angle class Ⅰ. To define the final occlusion in virtual environment, two steps were included: (1) The morphology data of upper and lower dentition were digitalized by surface scanner (Smart Optics/Activity 102; Model-Tray GmbH, Hamburg, Germany); (2) the virtual relationships were defined using 3Shape software. The control standard of final occlusion was manually defined using gypsum models and then digitalized by surface scanner. The final occlusion of test group and control standard were overlapped according to lower dentition morphology. Errors were evaluated by calculating the distance between the corresponding reference points of testing group and control standard locations.Results: The overall errors for upper dentition between test group and control standard location were (0.51±0.18) mm in non-tooth-extracted test group and (0.60±0.36) mm in tooth-extracted test group. The errors were significantly different between these two test groups ( P<0.05). However, in both test groups, the errors of each tooth in a single dentition does not differ from one another. There was no significant difference between errors in tooth-extracted test group and 1 mm ( P>0.05); and the accuracy of non-tooth-extracted group was significantly smaller than 1 mm ( P<0.05).Conclusion: The error of virtual occlusal definition of none class I molar relationship is higher than that of class I relationship, with an accuracy of 1 mm. However, its accuracy is still feasible for clinical application.

Key words: Computer-assisted surgical simulation; Orthognathic surgery; Virtual occlusion definition; Angle class Ⅰ molar relationship;

计算机辅助手术模拟进行正颌外科手术设计已经广泛应用于临床[1, 2, 3, 4, 5, 6, 7, 8], 与传统的模型外科相比, 其主要优势在于:(1)将咬合关系的改变与颌骨形态相关联, 有利于术者更准确地控制患者术后骨骼形态; (2)简化术前设计准备流程, 去除面弓转移、模型外科、咬合导板捏制等手工操作流程, 提高治疗精度。然而, 目前计算机辅助的数字化模拟手术设计流程中, 终末咬合关系的确定依旧依赖传统技术, 医生在石膏模型上拼对终末咬合关系, 再采用扫描仪将其数字化, 而后通过配准融合等数据处理步骤与颌骨数据进行融合[8], 此方法的缺陷在于操作过程复杂, 费时费力, 且经过多次数据配准转换, 易造成误差; 此外, 医生确立终末咬合关系时无法看到咬合的轻微改变引起的骨骼形态变化[9], 从而可能会影响手术效果预测的精确性。

2006年Pongrá cz等[9]首先报道了在虚拟环境中进行上下颌咬合匹配, 此后许多学者对于虚拟环境中咬合关系的确立进行了研究[10, 11, 12], 并证实虚拟环境中确定的咬合关系的精确度约为1 mm, 满足临床要求[10]。本课题组的前期研究通过可视化分析优化了虚拟终末咬合关系确定的技术流程, 并证实其精度满足临床要求[13]。但是国外学者和本课题组的前期研究均建立在磨牙关系正常的基础上, 而相当多的正颌外科患者在术前正畸阶段, 为了获得满意的上下颌骨相对移动幅度, 或者为去除牙轴代偿、解除拥挤等, 需拔除双侧各一个上颌双尖牙, 造成了上下颌牙齿数量不匹配, 终末咬合关系并非磨牙中性关系, 在这样的磨牙非中性关系中, 磨牙区尖窝交错关系改变, 可能降低虚拟环境确立的咬合关系精度, 但目前尚未见相关报道, 因此, 本研究旨在检测磨牙非中性关系时虚拟咬合拼对的精度及临床可行性。

1 材料与方法

选取20副完成术前正畸, 牙弓形态协调, 达到正颌外科手术标准的寄存石膏模型, 其中10副无正畸减数拔牙, 终末咬合关系为中性磨牙关系, 设为非拔牙组; 另外10副正畸减数拔除上颌双侧各一个双尖牙, 终末咬合关系为磨牙非中性关系, 设为拔牙组。

排除标准:(1)存在畸形牙者; (2)需分块截骨者; (3)存在正畸减数牙以外的牙列缺损者; (4)存在未关闭的牙间隙者。

1.1 数字化模型的获取

使用精度0.1 mm的3D扫描仪(Smart Optics/Activity 102; Model-Tray GmbH, Hamburg, Germany)对记存的上下牙列石膏模型进行扫描, 并以STL文件保存。

1.2 终末咬合关系的实测值获取

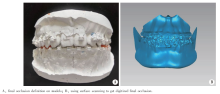
由一名正颌外科专业高年资医生将上下颌牙列石膏模型进行整体拼对, 确立终末咬合关系, 并使用硅橡胶咬合记录固定, 使用3D扫描仪扫描咬合关系, 以STL文件储存, 作为术后咬合关系的“ 实测值” (图1)。

图1 咬合关系“ 实测值” Figure 1 Control standard of final occlusion

1.3 虚拟终末咬合关系建立的流程

由同一名医生在3Shape软件环境下对拔牙组和非拔牙组模型进行虚拟终末咬合关系拼对。拼对咬合关系时, 保证下颌牙列不动, 单纯移动上颌骨模型进行初步拼对, 依据为:(1)上下颌牙弓形态基本匹配; (2)切牙形成正常覆盖及覆牙合关系; (3)尖窝关系基本匹配, 拔牙组达到尖牙中性关系, 非拔牙组达到磨牙中性关系; (4)上下颌牙列间无咬合碰撞点。当上述4个条件基本满意时, 再进行精细调整, 方法为:使上颌牙列逐步靠近下颌牙列, 至上下颌牙列至少同时存在3个碰撞检测点(即接触点), 其中双侧磨牙区各1个, 前牙区1个; 如无法达到该条件, 返回初步拼对进行进一步调整, 再进行精细调整, 直至满足上述条件为止; 而后撤回最后一步操作, 使得上下颌牙列无接触点, 保证上下颌牙列间无相交, 以排除术后咬合早接触点。完成终末咬合关系的建立, 导出上下颌牙列STL文件, 作为测试数据(图2)。

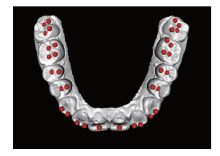
图2 虚拟环境终末咬合的建立Figure 2 Occlusal definition in virtual environment

1.4 评估误差

使用Mimics软件, 于上颌牙列模型上定义尖窝标志点[13](图3), 测量实验位置与“ 实测值” 上颌牙列中同一标志点的三维距离d(mm), 对每颗牙上的标记点误差求均值, 作为每颗牙虚拟环境与“ 实测值” 之间的误差。

图3 上颌尖窝标志点Figure 3 Marker points on maxilla

1.5 统计学分析

使用SPSS 20.0 进行统计学分析, 计算每个患者全牙列平均误差, 检验正态分布齐性后, 使用单样本t检验比较与临床可接受精确度1 mm间是否存在统计学差异, 使用ANOVA单因素分析同一上颌牙列中每颗牙之间是否存在统计学差异; 使用ANOVA单因素分析拔牙组和非拔牙组的平均误差是否具有统计学差异。P< 0.05认为差异具有统计学意义。

2 结果

拔牙组患者全牙列平均误差为(0.60± 0.36) mm, 每颗牙平均误差为0.52~0.77 mm(表1)。非拔牙组患者全牙列平均误差为(0.51± 0.18) mm, 每颗牙平均误差为0.46~0.61 mm(表2)。

拔牙组患者(C1~C10)中, 正态分布检测齐性(P > 0.05), 单样本t检验显示: C1、C4、C5全牙列平均误差与1 mm差异无统计学意义, 剩余各组与 1 mm差异有统计学意义, 且误差平均值小于1 mm(表3), 该结果表明拔牙组的平均误差与1 mm差异无统计学意义, 此外, 每颗牙之间差异无统计学意义(F=0.342, P > 0.05, 表4)。

非拔牙组患者(C11~C20)全牙列平均误差正态分布检测齐性(P > 0.05), 单样本t检验与1 mm之间差异有统计学意义, 且误差平均值小于1 mm(表5), 该结果表明, 非拔牙组与实测值间的误差显著小于1 mm。此外, 每颗牙之间差异无统计学意义(F=0.445, P > 0.05, 表6)。

拔牙组与非拔牙组之间平均误差差异有统计学意义(F=6.49, P < 0.05, 表7)。

表1 拔牙组与实测值间单颗牙平均误差 Table 1 Average errors of each tooth for tooth-extracted test group and control standard /mm
表2 非拔牙组与实测值间单颗牙平均误差 Table 2 Average errors of each tooth for non-tooth-extracted test group and control standard /mm
表3 拔牙组均值与1 mm之间单样本t检验 Table 3 One-sample test between the errors for each model and 1 mm in tooth-extracted test group
表4 拔牙组每颗牙误差ANOVA分析 Table 4 Differences in the errors of each teeth in tooth-extracted test group
表5 非拔牙组均值与1 mm之间单样本t检验 Table 5 One-sample test between the error for each model and 1 mm in non-tooth-extracted test group
表6 非拔牙组每颗牙误差ANOVA分析 Table 6 Differences in the errors of each teeth in non-tooth-extracted test group
表7 拔牙组与非拔牙组之间平均误差的ANOVA检验 Table 7 Differences in the errors beween tooth-extracted test group and non-tooth-extracted group
3 讨论

在石膏模型上进行终末咬合关系建立的过程中, 医生主要参考的是切牙覆牙合及覆盖关系、磨牙关系及尖窝接触的稳定性等。在虚拟环境下确立咬合关系, 同样以这些标准作为参考。在Pongrá cz等[9]的研究中, 由于部分样本第一磨牙缺失, 通过确定第二前磨牙关系和中切牙对应关系确立终末咬合关系, 但因为算法中并未引入碰撞检测, 因而虚拟重建的咬合关系可能与真实情况存在较大差异。Nadjmi等[10]在此基础上引入碰撞检测算法, 首次建立了精度满足临床要求的虚拟终末咬合的技术流程。本课题组的前期研究中, 引入视觉分析的技术, 通过矢量标记、碰撞接触点和尖窝对应关系参考辅助虚拟咬合重建过程[13]。在Pongrá cz等[9]和 Nadjmi等[10]的研究中, 为排除第一磨牙缺失造成的磨牙关系缺失, 使用第二前磨牙尖窝关系代替中性磨牙关系作为咬合建立的重要参考, 在本课题组前期研究中, 磨牙中性关系则是虚拟环境下咬合建立的直接参考。

对于大部分牙颌面畸形的患者而言, 往往在术前正畸阶段需拔除上颌左右各一个双尖牙, 以获得足够的间隙去除牙轴代偿, 解除牙列拥挤, 为上下颌骨关系的改变提供足够的覆盖或反覆盖, 可见, 磨牙非中性关系在正颌外科患者终末咬合关系中具有一定普遍性, 因此, 评价磨牙非中性关系的虚拟咬合重建精度, 是评价虚拟咬合重建流程能否满足正颌外科临床需求的必要条件之一。

在本课题组前期研究中, 证实了本研究采用的虚拟重建咬合技术流程对于磨牙中性关系模型虚拟重建的误差与1 mm差异无统计学意义[13], 在此基础上, 本研究对于磨牙非中性关系对虚拟咬合重建精度影响进行探讨。

基于本研究结果, 拔牙组和非拔牙组的平均误差差异具有统计学意义, 前者大于后者, 通过每颗牙的误差均值统计学比较发现, 拔牙组单颗牙误差均大于非拔牙组, 且不存在磨牙区与非磨牙区的差异, 另外, 拔牙组的标准差普遍大于非拔牙组, 说明其每颗牙的误差值波动较大, 出现本结果的原因可能是拔牙组患者减数拔牙后, 上下颌不匹配, 拔牙使得磨牙区尖窝关系出现变化, 无法达到标准Angle Ⅰ 类的中性咬合关系, 造成虚拟环境中确立稳定咬合位置相对困难, 因此其误差值相对较大, 同时离散性也更高, 但其误差值与1 mm间差异无统计学意义。以往的研究结果表明[10, 13], 正颌外科终末关系误差1 mm为临床可接受, 基于这一标准, 本研究结果证实磨牙非中性关系的虚拟咬合重建满足临床要求。

本研究尚存在一定的局限性, 首先, 本实验仅实现了对于单纯Le Fort Ⅰ 型截骨术患者在虚拟环境中确立终末咬合关系的流程, 并验证其精度, 未考虑需要进行分块Le Fort Ⅰ 型截骨术以改善切牙牙轴、匹配上下牙列牙弓宽度的患者; 其次, 本实验仅验证了对于同一实验者而言, 虚拟环境及石膏模型实现的终末咬合间不存在统计学差异, 对于不同操作者而言, 流程是否存在操作者间差异、该差异是否为临床可接受尚未验证; 另外, 本实验临床患者数量较少, 仅为初步的探索性研究, 是否可应用于临床尚需进一步大样本量、多实验者验证。

综上所述, 磨牙非中性关系虚拟咬合拼对的误差值高于磨牙中性关系虚拟咬合拼对的误差值, 但其精度满足临床需求, 具备临床应用价值。

The authors have declared that no competing interests exist.

参考文献
[1] Lin HH, Lo LJ. Three-dimensional computer-assisted surgical simulation and intraoperative navigation in orthognathic surgery: a literature review[J]. J Formos Med Assoc, 2015, 114(4): 300-307. [本文引用:1]
[2] Kang SH, Kim MK, You TK, et al. Modification of planned postoperative occlusion in orthognathic surgery, based on computer- aided design/computer-aided manufacturing-engineered preoperative surgical simulation[J]. Int J Oral Maxillofacial Surg, 2014, 73(1): 134-151. [本文引用:1]
[3] Varga E Jr, Hammer B, Hardy BM, et al. The accuracy of three-dimensional model generation: What makes it accurate to be used for surgical planning[J]. Int J Oral Maxillofacial Surg, 2013, 42(9): 1159-1166. [本文引用:1]
[4] Marchiori EC, Garcia RR, Moreira RW. Importance of occlusal plane reproduction on the semi-adjustable articulator in planning maxillary impactions for orthognathic surgery[J]. Int J Oral Maxil-lofacial Surg, 2013, 17(2): 109-114. [本文引用:1]
[5] Aboul-Hosn Centenero S, Ternand ez-Alfaro F. 3D planning in orthognathic surgery: CAD/CAM surgical splints and prediction of the soft and hard tissues results: our experience in 16 cases[J]. Cranio Maxillo Facial Surg, 2012, 40(2): 162-168. [本文引用:1]
[6] Gateno J, Xia JJ, Teichgraeber JF. New methods to evaluate craniofacial deformity and to plan surgical correction[J]. Semin Orthod, 2011, 17(3): 225-234. [本文引用:1]
[7] Xia J, Ip HH, Samman N, et al. Computer-assisted three-dimensional surgical planning and simulation: 3D virtual osteotomy[J]. Int J Oral Maxillofacial Surg, 2000, 29(4): 250-258. [本文引用:1]
[8] Chapuis J, Schramm A, Pappas I, et al. A new system for computer-aided preoperative planning and intraoperative navigation during corrective jaw surgery[J]. IEEE Trans Inf Technol Bio-med, 2007, 11(3): 274-287. [本文引用:2]
[9] Pongrácz F, Bárdosi Z. Dentition planning with image-based occlusion analysis[J]. Int J CARS, 2006, 1(1): 149-156. [本文引用:4]
[10] Nadjmi N, Mollemans W, Daelemans A, et al. Virtual occlusion in planning orthognathic surgical procedures[J]. Int J Oral Ma-xillofacial Surg, 2010, 39(5): 457-462. [本文引用:5]
[11] Stavness IK, Hannam AG, Tobias DL, et al. Simulation of dental collisions and occlusal dynamics in the virtual environment[J]. J Oral Rehabil, 2015, 43(4): 269-278. [本文引用:1]
[12] Maruyama T, Nakamura Y, Hayashi T, et al. Computer-aided determination of occlusal contact points for dental 3-D CAD[J]. Med Bio Eng Comput, 2006, 44(5): 445-450. [本文引用:1]
[13] Liu XJ, Li QQ, Zhang Z, et al. Virtual occlusal definition for orthognathic surgery[J]. Int J Oral Maxillofacial Surg, 2015, 45(3): 406-411. [本文引用:5]