引用本文
蔺轲, 谢俊卿, 胡永华, 孔桂兰. 支持向量机在ICU急性肾损伤患者住院死亡风险预测中的应用. 北京大学学报(医学版), 2018,50(2): 239-244
LIN Ke, XIE Jun-qing, HU Yong-hua, KONG Gui-lan. Application of support vector machine in predicting in-hospital mortality risk of patients with acute kidney injury in ICU. Journal of Peking University(Health Sciences), 2018,50(2): 239-244.  
Doi: 10.3969/j.issn.1671-167X.2018.02.007
Permissions
Copyright©2018, 北京大学
《北京大学学报(医学版)》编辑部 所有
支持向量机在ICU急性肾损伤患者住院死亡风险预测中的应用
蔺轲1,2, 谢俊卿1,2, 胡永华1,2, 孔桂兰2,△
1. 北京大学公共卫生学院流行病与卫生统计学系, 北京 100191
2. 北京大学医学信息学中心, 北京 100191
收稿日期: 2017-11-30
资助项目: 国家自然科学基金(81771938,81301296)、北京大学临床+X项目(PKU2017LCX05)和北京大学医学-信息科学交叉学科种子基金项目(BMU20160592)资助
摘要
目的:应用支持向量机(support vector machine,SVM)构建ICU中急性肾功能损伤(acute kidney injury, AKI)患者住院死亡风险预测模型,并比较其与ICU中常用的简化急性生理评分(the simplified acute physiology score Ⅱ,SAPS-Ⅱ)的预测性能。方法:使用重症监护医学信息市场(medical information mart for intensive care Ⅲ,MIMIC-Ⅲ)数据库作为数据来源。根据2012年国际改善全球肾脏病预后组织(Kidney Disease: Improving Global Outcomes, KDIGO)发表的《急性肾损伤临床实践指南》选取MIMIC-Ⅲ数据库中的AKI患者,使用SAPS-Ⅱ中所用到的全部变量构建SVM模型,同时,使用MIMIC-Ⅲ数据库定制本地化的SAPS-Ⅱ模型,并比较其与SVM模型的性能优劣。模型性能的评价方法使用五折交叉验证,评价指标使用受试者工作特征曲线下面积(area under the receiver operation characteristic curve,AUROC)、均方根误差(root mean squared error,RMSE)、灵敏度、特异度和准确率。此外,使用Bland-Altman图评估两模型预测结果的一致性。结果:共纳入19 044例AKI患者,死亡率为13.58%。五折交叉验证的结果显示,SVM模型和定制版SAPS-Ⅱ模型的平均AUROC分别为0.86和0.81, 差异有统计学意义( t=13.0, P<0.001), SVM模型和定制版SAPS-Ⅱ模型的平均RMSE分别为0.29和0.31, 差异有统计学意义( t=-9.6, P<0.001)。在灵敏度和约登指数方面,SVM模型也均优于定制版的SAPS-Ⅱ模型,差异均具有统计学意义( P分别为0.002和<0.001)。Bland-Altman图显示当患者死亡风险极高或者极低时,两模型预测结果的一致性较好。当患者死亡风险的不确定性较大时,两模型预测结果的一致性较差。结论:相比于传统的SAPS-Ⅱ模型,SVM模型的预测性能更优,且当患者的死亡风险不确定时,这种优势尤其明显; SVM模型更有利于AKI患者的死亡风险识别与早期干预,能有效地帮助ICU临床医生提高医疗质量,有很强的临床应用价值。
关键词: 重症监护室; 急性肾损伤; 死亡风险预测; 支持向量机
中图分类号:R181.2 文献标志码:A 文章编号:1671-167X(2018)02-0239-06
Application of support vector machine in predicting in-hospital mortality risk of patients with acute kidney injury in ICU
LIN Ke1,2, XIE Jun-qing1,2, HU Yong-hua1,2, KONG Gui-lan2,△
1. Department of Epidemiology and Biostatistics, Peking University School of Public Health, Beijing 100191, China
2. Medical Informatics Center, Peking University, Beijing 100191, China
△ Corresponding author’s e-mail, guilan.kong@hsc.pku.edu.cn
Fund:Supported by the National Natural Science Foundation of China(81771938,81301296), Peking University Clinical Medicine + X Project (PKU2017LCX05) and Peking University Seed Fund for Medicine-Information Interdisciplinary Research Project (BMU20160592)
Abstract
Objective:To construct an in-hospital mortality prediction model for patients with acute kidney injury (AKI) in intensive care unit (ICU) by using support vector machine (SVM), and compare it with the simplified acute physiology score Ⅱ (SAPS-Ⅱ) which is commonly used in the ICU.Methods:We used Medical Information Mart for Intensive Care Ⅲ (MIMIC-Ⅲ) database as data source. The AKI patients in the MIMIC-Ⅲ database were selected according to the 2012 Kidney Disease: Improving Global Outcomes (KDIGO) definition of AKI. We employed the same predictor variable set as used in SAPS-Ⅱ to construct an SVM model. Meanwhile, we also developed a customized SAPS-Ⅱ mo-del using MIMIC-Ⅲ database, and compared performances between the SVM model and the customized SAPS-Ⅱ model. The performance of each model was evaluated via area under the receiver operation characteristic curve (AUROC), root mean squared error (RMSE), sensitivity, specificity, Youden’s index and accuracy based on 5-fold cross-validation. The agreement of the results between the SVM mo-del and the customized SAPS-Ⅱ model was illustrated using Bland-Altman plots.Results:A total number of 19 044 patients with AKI were included. The observed in-hospital mortality of the AKI patients was 13.58% in MIMIC-Ⅲ. The results based on the 5-fold cross validation showed that the average AUROC of the SVM model and the customized SAPS-Ⅱ model was 0.86 and 0.81, respectively (The difference between the two models was statistically significant with t=13.0, P<0.001). The average RMSE of the SVM model and the customized SAPS-Ⅱ model was 0.29 and 0.31, respectively (The difference was statistically significant with t=-9.6, P<0.001). The SVM model also outperformed the customized SAPS-Ⅱ model in terms of sensitivity and Youden’s index with significant statistical differences ( P = 0.002 and <0.001, respectively).The Bland-Altman plot showed that the SVM model and the custo-mized SAPS-Ⅱ model had similar mortality prediction results when the mortality of a patient was certain, but the consistency between the mortality prediction results of the two models was poor when the mortality of a patient was with high uncertainty.Conclusion:Compared with the SAPS-Ⅱ model, the SVM model has a better performance, especially when the mortality of a patient is with high uncertainty. The SVM model is more suitable for predicting the mortality of patients with AKI in ICU and early intervention in patients with AKI in ICU. The SVM model can effectively help ICU clinicians improve the quality of me-dical treatment, which has high clinical value.
Key words: Intensive care unit; Acute kidney injury; Mortality prediction; Support vector machine

急性肾功能损伤(acute kidney injury, AKI)是住院患者常见的危重症之一。AKI患者具有较高的死亡率和发展为慢性肾脏病的风险[1]。虽然近年来的诊疗水平不断提高, 但AKI所带来的疾病负担仍然十分沉重, 这一情况在重症监护室(intensive care unit, ICU)尤为严重[2], 因此, 评价ICU中AKI患者病情的严重程度并预测其住院死亡风险, 对AKI患者的死亡风险识别、评价ICU医疗质量和合理利用医疗资源均至关重要。急性生理学和慢性健康状况评分(the acute physiology and chronic health evaluation Ⅱ , APACHE-Ⅱ )[3]、简化急性生理评分(the simplified acute physiology score Ⅱ , SAPS-Ⅱ )[4]等ICU常用危重症病情评分系统是目前量化ICU中AKI患者住院死亡风险最常用的手段之一。然而, 近年来随着医疗信息化程度不断提高, 绝大多数诊疗信息能够以数字化形式得以保存, 这为开发新的死亡风险预测模型提供了可靠而丰富的数据来源。另一方面, 数据挖掘与机器学习技术的蓬勃发展为开发新的死亡风险预测模型提供了理论基础。支持向量机(support vector machine, SVM)是20世纪90年代中期由Vapnik等[5]根据结构风险最小化的原则提出的一种机器学习方法, 在ICU死亡风险预测领域得到了良好的应用[6]。SVM有坚实的统计学理论作为支撑, 与其他预测模型相比具有优越的预测性能[7]。目前缺乏使用SVM预测ICU中AKI患者死亡风险的研究, 因此, 本文以国外大型重症医疗数据库重症监护医学信息市场(medical information mart for intensive care Ⅲ , MIMIC-Ⅲ )为数据源, 利用SVM构建ICU中AKI患者的住院死亡风险预测模型, 并比较其与传统的SAPS-Ⅱ 评分系统的预测性能。

1 资料与方法
1.1 资料来源

本次研究的患者来自于MIMIC-Ⅲ 大型重症医疗数据库[8], 该数据库由美国麻省理工学院计算生理学实验室、美国哈佛医学院贝斯以色列迪康医学中心于2015年8月合作建立并维护, 存储了近5万例ICU患者的临床信息, 3亿多条结构化数据, 包括了每例患者人口学特征、诊断编码、实验室检验和检测结果、医疗干预记录、出院记录等。国内外基于MIMIC-Ⅲ 数据库的上一版本MIMIC-Ⅱ 已有大量的文献发表和科学发现, MIMIC-Ⅲ 数据库在MIMIC-Ⅱ 的基础上增加了2008— 2012年的数据, 并改善了数据质量。MIMIC-Ⅲ 数据库是重症医学领域临床研究的宝库, 其数据经过严格的去隐私处理并对全球研究人员免费开放。该数据库不仅样本量大、数据类型丰富, 而且数据质量好、可靠性高。

1.2 研究结局与预测变量

本研究的结局变量为ICU中AKI患者的存活状态, 模型预测的结果为每个AKI患者的住院死亡概率。本研究使用2012年国际改善全球肾脏病预后组织(Kidney Disease: Improving Global Outcomes, KDIGO)发表的《急性肾损伤临床实践指南》[9]作为AKI患者的诊断标准, 即:48 h内血肌酐增高≥ 26.5 μ mol/L; 或血肌酐增高至基线值的 1.5倍以上, 且明确或推测其在之前的7 d内发生; 或持续6 h 尿量0.5 mL/(kg· h)。血肌酐的基线值取患者入ICU后的第一次测量值。

为了更加客观地比较SVM和SAPS-Ⅱ 之间的性能, 本研究使用SAPS-Ⅱ 评分系统中所用到的全部变量构建SVM模型, 这些变量包括:入ICU后24 h 内的12 项生理指标、年龄、入院类型(计划手术、非计划手术、无手术), 以及是否合并艾滋病、转移癌、血液系统恶性肿瘤。在这些变量中, 某些生理指标是重复测量的, 例如心率、血压、体温等。这类重复测量变量由于数据量庞大, 不宜将每次测量的数据都放入模型。在构建SAPS-Ⅱ 模型的过程中, 我们按照SAPS-Ⅱ 原始文献[4]中所提供的方法对变量进行处理, 具体的处理方法为:对于只有唯一取值的变量, 如年龄、性别等变量, 根据变量的取值不同, 分别赋予不同的分值。对于重复测量的变量, 根据SAPS-Ⅱ 原始文献的规则选取该变量的最大值或最小值, 并据此赋予不同的分值。在构建SVM模型时, 对于只有唯一取值的变量, 我们直接取该变量的原始值, 对于重复测量的变量, 我们仅提取各个重复测量变量在入ICU后24 h内的最大值和最小值。

1.3 患者纳入和排除标准

(1)纳入标准:年龄≥ 18岁且≤ 90岁; 符合KDIGO诊断标准; (2)排除标准:一次住院期间多次入ICU的患者; 变量缺失率超过30%的患者。

1.4 预测模型

1.4.1 SVM模型 SVM的目标是在高维空间中创建一个最佳的分类边界(最大间隔超平面), 从而将不同类别的样本区分开来。最大间隔超平面是与其最接近的点之间的距离达到最大的分类边界。支持向量即指每个类中最接近最大间隔超平面的点[7, 10]。

以下为在给定特征空间上包含N个样本点的训练数据集:

T={(x1, y1), (x2, y2), …, (xN, yN)}(1)

其中, (xi, yi)称为第 i个样本点, xi∈Rn, yi∈{+1, -1}。当 yi为+1时, xi被称为正类; 当 yi为-1时, xi被称为负类。SVM学习的目标是在特征空间中找到一个分离超平面, 可以将数据分为两类:正类和负类。

SVM中的决策函数可以如下表示:

h(x)=wTφ(x)+b(2)

其中, w代表了分离超平面的法向量, φ(x)代表了将样本 x从输入空间映射高维特征空间的函数, b为模型偏置。

SVM分类器需要满足以下条件:

wTφ(xi)+b≥1当yi=+1wTφ(xi)+b≤-1当yi=-1(3)

等式 wTφ(xi)+b=0代表了学习到的分离超平面, 但当训练数据不是线性可分时, 样本点 (xi, yi)不能满足式(3)中函数间隔≥ 1的约束条件, 因此, 需要将约束条件中的硬间隔变为软间隔, 引入了弛度变量 ξi来实现软间隔, 此时SVM的学习问题变为如下凸二次规划问题:

minw, b, ξ12wTw+C∑i=1Nξisubjecttoyi(wTφ(xi+b))≥1-ξiξi≥0, i=1, 2, …, N(4)

其中, C是惩罚参数, C值越大对误分类的惩罚增大, C值越小对误分类的惩罚减小。 ξi用来引入软间隔, φ(x)代表了从输入空间非线性映射到特征空间的函数。通过引入拉格朗因子 ai, 问题(4)的对偶问题如式(5)所示。在线性不可分的情况下, 求解得到的 αi> 0的样本点 (xi, yi)的实例 x称为支持向量(软间隔的支持向量), 它决定了决策函数。

maxαi∑i=1Nαi-12∑i=1N∑j=1Nαiαjyiyjk(xi, xj)subjectto∑i=1Nαiyi=0, 0≤αi≤C, i=1, 2, …, N(5)

其中, k(xi, xj)=< φ (xi), φ (xj)> , 是将输入向量映射到特征空间的核函数。当对偶问题解决后, SVM决策函数可以表达为:

h(x)=wTφ(x)+b=∑i=1Naiyik(xi, x)+b=∑i∈svNaiyik(xi, x)+b(6)

本研究利用R软件中的kernlab软件包进行SVM建模, 惩罚参数设为1, 核函数采用径向基函数。预测变量为SAPS-Ⅱ 模型中各变量的原始值, 其中重复变量包含最大值和最小值。输出结果为每个AKI患者的住院死亡概率。

1.4.2 SAPS-Ⅱ 模型 SAPS-Ⅱ 是一个基于Logistic回归开发的危重症评分系统, 被广泛地用于评估ICU患者病情严重程度和死亡风险, 具体的使用方法为:根据患者的情况, 对SAPS-Ⅱ 中各个变量进行打分, 然后计算每个患者的总得分, 进而根据原始文献中提供的公式计算出每个患者的住院死亡风险。具体的公式如下:

logit=β0+β1×(SAPSⅡscore)+β2×[ln(SAPSⅡscore+1)](7)

Poriginal=elogit/1+elogit(8)

其中, β0, β1, β2为原始文献中给出的系数, SAPSⅡscore为SAPS-Ⅱ 模型中各变量得分值的总和, Poriginal为SAPS-Ⅱ 模型预测的患者的死亡风险。

1.4.3 定制版SAPS-Ⅱ 模型 由于SAPS-Ⅱ 开发于20世纪90年代, 各变量的系数是基于当时的ICU人群计算得来, 故将SAPS-Ⅱ 模型直接应用于目前的ICU人群时, 模型的性能往往不如人意。一个可行的解决办法是使用当前数据定制本地化的模型, 即以患者的结局为因变量, 以SAPS-Ⅱ 模型中各变量的得分值为自变量, 建立Logistic回归模型, 进而以该回归模型的系数计算患者的死亡风险。本研究参照Moreno等[11]的方法用MIMIC-Ⅲ 数据库定制了SAPS-Ⅱ 模型, 并将定制版的SAPS-Ⅱ 模型作为SVM模型的比较对象。具体的定制方法为:

New logit= β'0+β'1×(age score) + β'2×(heart rate score) …+ β'15×(comorbidity score)(9)

Pcustomized=elogit/1+elogit(10)

其中, β'0, β'1, β'2…β'15为根据当前的数据计算的各变量的系数, age score, heart rate score等为SAPS-Ⅱ 模型中各变量的得分值。 Pcustomized为定制版的SAPS-Ⅱ 模型预测的患者的死亡风险。

1.5 统计分析与模型比较

数据的提取与清洗使用PostgreSQL数据库, 数据分析与模型建立使用R软件。各变量的缺失值用该变量的均值替代。模型性能的评价使用五折交叉验证, 即将现有的数据随机分为5等份, 每一份都单独作为测试集, 其余4份作为训练集。在训练集中分别利用SVM、SAPS-Ⅱ 和定制版SAPS-Ⅱ 构建预测模型, 在测试集中计算受试者工作特征(receiver operation characteristic, ROC)曲线下面积(area under the ROC curve, AUROC)、均方根误差(root mean squared error, RMSE), 并通过ROC曲线确定最佳截断值, 从而计算灵敏度、特异度、约登指数和准确率。模型进行性能比较时, 我们取5次结果的平均值进行比较。使用配对t检验评价各模型5次结果之间的差异是否有统计学意义。另外, 为了更深入地探究SVM模型与SAPS-Ⅱ 模型预测性能的差异所在, 我们使用Bland-Altman分析评价了两模型预测性能之间的一致性。Bland-Altman分析是一种以图形化的方式评价两种测量手段结果一致性的方法, 被广泛用于放射医学、超声医学、实验室医学等临床领域, 该方法既能分析不同预测模型的一致性, 亦能找出不同预测模型之间的差异性所在。

2 结果
2.1 AKI数据的基本特征

经过数据清洗, 本研究共纳入19 044例AKI患者, 死亡率为 13.58%, 平均年龄(63.75± 16.13)岁, 男性患者有11 202例, 占比58.82%。患者的平均SAPS-Ⅱ 得分为(38.95 ± 14.53)分。患者的详细信息见表1。

表1 AKI数据的基本特征 Table 1 Characteristics of AKI data in MIMIC-Ⅲ
2.2 模型的性能比较结果

SVM模型、SAPS-Ⅱ 模型和定制版SAPS-Ⅱ 模型的预测性能见表2, 可以看出SVM模型在AUROC、RMSE和约登指数方面的表现均为最优。对于SAPS-Ⅱ 模型, 经过定制之后, SAPS-Ⅱ 模型的预测性能有了一定的提升, AUROC由 0.79提升至 0.81, 约登指数由0.45提升至0.47, 准确率由0.74提升至0.76, RMSE由0.36降低至0.31, 但是定制版的SAPS-Ⅱ 模型的预测性能还是弱于SVM模型, 其AUROC比SVM模型低约0.05, 差异具有统计学意义。在RMSE方面, SVM模型优于定制版SAPS-Ⅱ 模型, 差异具有统计学意义。此外, SVM模型在灵敏度和约登指数方面也均优于定制版的SAPS-Ⅱ 模型, 差异均具有统计学意义。

表2 3种模型的预测性能比较 Table 2 Comparison of performance of three models
2.3 Bland-Altman分析结果

Bland-Altman见图1, 横坐标为SVM模型和定制版SAPS-Ⅱ 模型预测的患者死亡概率的平均值, 该值作为患者的死亡风险; 纵坐标为SVM模型和定制版SAPS-Ⅱ 模型预测的患者的死亡概率的差值。当患者的死亡风险极低或者极高时, SVM模型和定制版SAPS-Ⅱ 模型的预测结果的一致性很高, 但当患者的死亡风险为50%左右时, 两模型预测结果的一致性很差。

图1 Bland-Altman图Figure 1 Bland-Altman plot

3 讨论

传统的AKI患者死亡风险评价工具主要是各类危重症病情评分系统, 主要包括APACHE-Ⅱ 、SAPS-Ⅱ 等ICU通用病情评分系统, 也有学者尝试为ICU的AKI患者中开发新的死亡风险评价工具[12], 但这些工具都是基于Logistic回归模型开发, 对复杂情况(如变量间的多重共线性)及高维数据的处理能力较差。机器学习技术的发展给我们提供了解决这一问题的全新思路。饶飘雪等[13]使用SVM、人工神经网络、Logistic回归建立了3个用于预测乳腺癌复发的模型, 结果显示相对于Logistic回归模型, SVM和人工神经网络具有更好的预测性能, 其中SVM的预测性能最好。Lee等[14]使用了16个变量分别建立了用于预测老年慢性病患者服药依从性的SVM模型和Logistic回归模型, 结果显示SVM模型和Logistic模型的分类准确率分别是97.3%和71.1%。

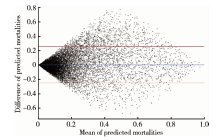
本研究我们使用SVM开发了用于预测ICU中AKI患者死亡风险的模型, 并比较其与定制版SAPS-Ⅱ 模型的预测性能。首先, 相对于原始的SAPS-Ⅱ 模型, 定制版SAPS-Ⅱ 模型的性能有了提升, 这说明定制版SAPS-Ⅱ 模型可以更深刻地理解当前数据背后的临床意义, 并且能更好地拟合数据。其次, 在性能指标AUROC和约登指数方面, SVM模型明显优于定制版SAPS-Ⅱ 模型, 差异具有统计学意义。在RMSE方面, SVM模型亦有优势。第三, 通过Bland-Altman分析, 我们发现这主要是大部分AKI患者的死亡风险集中在20%以内, 此时SVM和定制版SAPS-Ⅱ 模型预测结果的一致性较好, SVM模型的优势未能充分体现。但当患者的死亡风险接近50%时, 即死亡风险不确定时, SVM模型和定制版的SAPS-Ⅱ 模型预测结果的一致性很差。结合两模型的AUROC和约登指数的表现, 我们认为SVM模型的性能优于定制版SAPS-Ⅱ 模型, 且当患者的死亡风险不确定时, 这种优势尤其明显。

本研究开发的SVM模型在预测AKI患者的死亡风险方面有很强的临床应用价值。AKI患者往往病情复杂, 死亡率较高。本研究中的AKI患者的死亡率为13.58%, 这与一些AKI的流行病学研究中所报告的死亡率相近[15, 16]。AKI的早期发现和治疗可以改善预后, 降低死亡率, 这一点可以从AKI诊断标准的产生和演变中体现。在AKI的概念提出之前, 普遍使用的概念是急性肾衰竭, 但急性肾衰竭的各种诊断标准都忽视了早期肾损害的病理生理变化, 故而被淘汰。随后提出的危险、损伤、衰竭、肾功能丧失和终末期肾病(risk, injury, failure, loss, end-stage kidney disease, RIFLE)分级诊断标准、急性肾损伤网络(Acute Kidney Injury network, AKIN)分期标准和KDIGO诊断标准都越来越强调AKI的早期诊断与治疗。本研究提供的基于机器学习的SVM模型拥有比传统模型更优秀的预测性能, 更有利于AKI患者的死亡风险识别与早期干预。除此之外, 在临床科研方面, 还可以通过预测的死亡风险来对患者分组, 从而控制组间的可比性。

当然, 本研究亦有不足之处。首先, 尽管MIMIC-Ⅲ 数据库是一个高质量的数据来源, 但它只是一个基于美国人群的单中心数据库, 因此所得结论在模型外推方面存在一定的局限性, 其预测效果在其他人群, 尤其是中国人群的适用性仍需多中心的外部验证。由于伦理限制及硬件条件限制, 本次研究尚未获取到国内ICU中AKI患者的数据, 我们下一步研究将着眼于用中国人群的数据验证SVM模型的预测性能。其次, 基于数据变量的限制, 本研究未引入APACHE-Ⅱ 评分。以往有研究表明[17]APACHE-Ⅱ 评分系统对AKI患者预后的判断价值比SAPS-Ⅱ 更优。Luaces等[18]的研究发现, 在预测ICU患者死亡率方面, SVM模型的性能优于APACHE。由于MIMIC-Ⅲ 数据库中缺少APACHE-Ⅱ 的部分变量, 本研究未能对比SVM模型、APACHE-Ⅱ 和SAPS-Ⅱ 三者的性能。

综上所述, 相比于传统的SAPS-Ⅱ 模型, SVM模型的性能更优, 更适合预测ICU中AKI患者死亡风险。我们推荐在当前大数据时代, 临床医疗信息化程度很高的情形下, 应用计算机化的、基于SVM的住院死亡风险预测系统来辅助ICU医生进行临床决策和干预, 能够有效地帮助ICU内临床医生降低医疗差错、提高医疗质量。

The authors have declared that no competing interests exist.

参考文献
[1] Lameire NH, Bagga A, Cruz D, et al. Acute kidney injury: An increasing global concern[J]. Lancet, 2013, 382(9887): 170-179. [本文引用:1]
[2] Hoste EAJ, Bagshaw SM, Bellomo R, et al. Epidemiology of acute kidney injury in critically ill patients: The multinational AKI-EPI study[J]. J Intensive Care Med, 2015, 41(8): 1411-1423. [本文引用:1]
[3] Turner JS, Potgieter PD, Linton DM. Severity of disease classification system[J]. Crit Care Med, 1991, 19(2): 301. [本文引用:1]
[4] Le GJ, Lemeshow S, Saulnier F. A new simplified acute physiology score (SAPS Ⅱ) based on a European/North american multicenter study[J]. JAMA, 1993, 270(24): 2957-2963. [本文引用:2]
[5] Vapnik V, Cortes C. Support vector networks[J]. Mach Learn, 1995, 20(3): 273-297. [本文引用:1]
[6] Houthooft R, Ruyssinck J, Van dHJ, et al. Predictive modelling of survival and length of stay in critically ill patients using sequential organ failure scores[J]. Artif Intell Med, 2015, 63(3): 191-207. [本文引用:1]
[7] 丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报, 2011, 40(1): 2-10. [本文引用:2]
[8] Johnson AEW, Pollard TJ, Shen L, et al. MIMIC-Ⅲ, a freely accessible critical care database[J]. Sci Data, 2016, 3: 160035. [本文引用:1]
[9] Kidney disease: Improving Global Outcomes (KDIGO) Acute Kidney Injury Work Group. Kdigo clinical practice guideline for acute kidney injury[J]. Kidney Int, 2012, 2: 1-138. [本文引用:1]
[10] 谢俊卿, 蔺轲, 孔桂兰. 重症监护室住院死亡风险的预测方法研究[J]. 计算机工程与应用, 2017, 53(20): 24-30. [本文引用:1]
[11] Moreno R, Apolone G. Impact of different customization strategies in the performance of a general severity score[J]. Crit Care Med, 1997, 25(12): 2001-2008. [本文引用:1]
[12] Demirjian S, Chertow GM, Zhang JH, et al. Model to predict mortality in critically ill adults with acute kidney injury[J]. Clin J Am Soc Nephrol, 2011, 6(9): 2114-2120. [本文引用:1]
[13] 饶飘雪, 叶枫. 基于Logistic回归、ANN、SVM的乳腺癌复发影响因素研究[J]. 计算机系统应用, 2016, 25(7): 259-263. [本文引用:1]
[14] Lee SK, Kang BY, Kim HG, et al. Predictors of medication adherence in elderly patients with chronic diseases using support vector machine models[J]. J Healthc Inform Res, 2013, 19(1): 33-41. [本文引用:1]
[15] 雷莹, 聂晟, 孙丹华, 等. 中国危重症住院患者急性肾损伤的流行病学分析[J]. 南方医科大学学报, 2016, 36(6): 744-750. [本文引用:1]
[16] Yang L, Xing G, Wang L, et al. Acute kidney injury in china: A cross-sectional survey[J]. Lancet, 2015, 386(10002): 1465. [本文引用:1]
[17] 余娇, 王繁麟, 童小文. 不同危重评分对急性肾功能衰竭预后判断价值[J]. 现代仪器与医疗, 2016, 22(2): 18-20. [本文引用:1]
[18] Luaces O, Taboada F, Albaiceta GM, et al. Predicting the probability of survival in intensive care unit patients from a small number of variables and training examples[J]. Artif Intell Med, 2009, 45(1): 63-76. [本文引用:1]