一种基于图塌缩的药物分子检索方法

引用本文

瞿经纬, 吕肖庆, 刘振明, 廖媛, 孙鹏晖, 王蓓, 汤帜. 一种基于图塌缩的药物分子检索方法. 北京大学学报(医学版), 2018,50(2): 368-374
QU Jing-wei, LV Xiao-qing, LIU Zhen-ming, LIAO Yuan, SUN Peng-hui, WANG Bei, TANG Zhi. A retrieval method of drug molecules based on graph collapsing. Journal of Peking University(Health Sciences), 2018,50(2): 368-374. 复制到剪切板

Doi: 10.3969/j.issn.1671-167X.2018.02.028
Permissions

《北京大学学报(医学版)》编辑部所有

一种基于图塌缩的药物分子检索方法

瞿经纬¹, 吕肖庆^1,^2,^△, 刘振明³, 廖媛¹, 孙鹏晖¹, 王蓓¹, 汤帜^1,²

1. 北京大学计算机科学技术研究所, 北京 100080

2. 数字出版技术国家重点实验室, 北京 100080

3. 北京大学药学院药物化学系, 北京 100191

收稿日期: 2017-12-01

资助项目: 国家自然科学基金(61573028、61673029)、新闻出版业科技与标准重点实验室(新闻出版智能媒体技术重点实验室)和北京大学医学-信息科学交叉学科种子基金项目(BMU20160579)资助

摘要

目的:为实现准确、高效的医药信息查询,本文探索了一种基于图结构的药物分子检索方法。方法:基于图结构的药物分子检索方法以接收智能终端的拍照或手绘作为输入,并将输入的结构式形式化为相应图结构,基于对图匹配效率的直接影响因素的分析,建立了结构式的一种紧凑有效的超图表示形式,其依据结构式的特点结合了子图匹配与频繁子图挖掘等方法对大图进行多级塌缩。为避免塌缩过程中子图交叠问题阻碍超图的准确构建,引入一种基于图同构的算法,借助子图之间交叠情况的分析,选择占优子图,利用多维度信息完成精确的分子匹配。结果:为证明检索方法的有效性,将本文检索方法和Wikipedia Chemical Structure Explorer(WCSE)进行检索准确率的对比,结果表明,本文方法的检索准确率更高,前10个检索结果的MAP(mean average precision)、DCG(discounted cumulative gain)、RBP(rank-biased precision)和ERR(expected reciprocal rank)四个指标均高于WCSE。上述指标的领先幅度分别为10%、1.41、6.42%、1.32%。进一步通过两个系统的具体检索结果实例对检索效果进行直观对比,发现本文方法在药物分子检索有效性方面更具优势,能为用户提供更为满意的检索结果。结论:本研究提出的基于图结构相似度的药物分子检索方法能够实现较为理想的检索结果,实验证明本检索系统具有可行性和有效性。

关键词: 信息存储和检索; 分子结构; 图结构; 超图; 算法

中图分类号:R-058 文献标志码:A 文章编号:1671-167X(2018)02-0368-07

A retrieval method of drug molecules based on graph collapsing

QU Jing-wei¹, LV Xiao-qing^1,^2,^△, LIU Zhen-ming³, LIAO Yuan¹, SUN Peng-hui¹, WANG Bei¹, TANG Zhi^1,²

1.Institute of Computer Science & Technology, Peking University, Beijing 100080, China;

2. State Key Laboratory of Digital Publishing Technology, Beijing 100080, China

3. Department of Medical Chemistry, Peking University School of Pharmaceutical Sciences, Beijing 100191, China

△ Corresponding author’s e-mail, lvxiaoqing@pku.edu.cn

Fund:Supported by National Natural Science Foundation of China (61573028, 61673029), Key Laboratory of Science, Technology and Standard in Press Industry (Key Laboratory of Intelligent Press Media Technology) and Peking University Seed Fund for Medicine-Information Interdisciplinary Research Project (BMU20160579)

Abstract

Objective:To establish a compact and efficient hypergraph representation and a graph-similarity-based retrieval method of molecules to achieve effective and efficient medicine information retrieval.Methods:Chemical structural formula (CSF) was a primary search target as a unique and precise identifier for each compound at the molecular level in the research field of medicine information retrieval. To retrieve medicine information effectively and efficiently, a complete workflow of the graph-based CSF retrieval system was introduced. This system accepted the photos taken from smartphones and the sketches drawn on tablet personal computers as CSF inputs, and formalized the CSFs with the corresponding graphs. Then this paper proposed a compact and efficient hypergraph representation for molecules on the basis of analyzing factors that directly affected the efficiency of graph matching. According to the characteristics of CSFs, a hierarchical collapsing method combining graph isomorphism and frequent subgraph mining was adopted. There was yet a fundamental challenge, subgraph overlapping during the collapsing procedure, which hindered the method from establishing the correct compact hypergraph of an original CSF graph. Therefore, a graph-isomorphism-based algorithm was proposed to select dominant acyclic subgraphs on the basis of overlapping analysis. Finally, the spatial similarity among graphical CSFs was evaluated by multi-dimensional measures of similarity.Results:To evaluate the performance of the proposed method, the proposed system was firstly compared with Wikipedia Chemical Structure Explorer (WCSE), the state-of-the-art system that allowed CSF similarity searching within Wikipedia molecules dataset, on retrieval accuracy. The system achieved higher values on mean average precision, discounted cumulative gain, rank-biased precision, and expected reciprocal rank than WCSE from the top-2 to the top-10 retrieved results. Specifically, the system achieved 10%, 1.41, 6.42%, and 1.32% higher than WCSE on these metrics for top-10 retrieval results, respectively. Moreover, several retrieval cases were presented to intuitively compare with WCSE. The results of the above comparative study de-monstrated that the proposed method outperformed the existing method with regard to accuracy and effectiveness.Conclusion:This paper proposes a graph-similarity-based retrieval approach for medicine information. To obtain satisfactory retrieval results, an isomorphism-based algorithm is proposed for dominant subgraph selection based on the subgraph overlapping analysis, as well as an effective and efficient hyper-graph representation of molecules. Experiment results demonstrate the effectiveness of the proposed approach.

Key words: Information storage and retrieval; Molecular structure; Graph structure; Hypergraph; Algorithms

文章图片

医药信息检索旨在服务于大型的医药数据库、信息库和知识库, 需要融合药学、信息检索和机器学习等跨领域的先进技术, 基于化学分子结构式的检索方法已成为医药信息检索的关键技术之一, 现有检索系统多采用间接方式简化对分子结构的描述, 其检索结果的准确度也相应地受到了影响。图相似性的比较可以充分利用分子的空间结构信息, 实现准确、高效的检索, 但图计算的复杂度一直阻碍着该方法的应用。图形识别技术可看作是基于内容的图像检索的一个分支。

针对化学分子结构式识别与检索的研究可被大致分成三类:基于序列的方法、基于分子指纹(molecular fingerprint)的方法和基于图的方法。许多生物和化学信息用连续字符串来表示分子, 如最具代表性的SMILES(Simplified Molecular Input Line Entry System)^[1]语言, 但此类编码方法忽略过多的结构信息。分子指纹^[2]是另一类简单的分子编码方式, 如拓扑指纹(topological fingerprints)^[3]将代表分子特征的键径转换为给定数量的连接键, 但分子指纹在精确描述空间结构方面仍有一些困难。图是在化学信息学和生物信息学领域中被广泛应用的一种通用的数据结构^[4], 但当分子结构式随着原子数增加变成大图后, 该方法会因计算代价的瓶颈而无法取得很好的实用性。为此, 研究人员一直在探索大图的简化方法或更加有效的特征转换方法。

基于图的方法可以分成四个子类, 即图描述符、基于相似性的图挖掘、图嵌入(graph embedding)以及图核方法。图描述符涉及的范围较广, 包括从一维的统计^[5]到二维的拓扑指数^[6], 再到复杂的三维描述^[7]。图挖掘旨在研究相似的化合物或者预测分子的物化和生物性质, 所应用的常规技术包括最大公共子图^[8]、频繁子图挖掘^[9]和编辑距离^[10]。图嵌入是指使用向量来表示图。为了将图与机器学习方法相结合, 需要将每一个图映射到一个显式的向量空间^[11]。在新的向量空间中, 被嵌入图通过所获编码进行差异比较^[12], 从而度量出属性的统计特征。在图嵌入方法中会因将图“ 压缩” 成简洁的向量表示而丢失部分结构信息, 为了避免这一严重缺陷, 图的核方法被提出。该类方法采用了更加完备的数学框架, 如把图之间的相似性测量定义为希尔伯特空间(Hilbert space)的点积运算。Gaü zè re等^[13]采用了由严格子树集定义的模式袋(bag of pattern), 即所有具有最多六个节点的标签树的集合。环信息在分子性质中具有特别的影响力。环模式核(cyclic pattern kernel)^[14]把一个图分解成一个具有环结构的集合和一个与不在环中的原子和边相对应的集合。

尽管研究人员已经对化学分子结构式进行了数十年的研究, 但仍存在诸多挑战, 比如在对大分子进行搜索时难以承受的计算代价, 以及缺少一种对结构分类的标准等。总体上看, 现有图匹配和图挖掘方法仅限于小分子结构, 难以处理大型分子数据集中的复杂结构, 此外, 虽然已有个别技术被用于图压缩、简化分子的结构信息, 但大多局限于有限的且是预定义的结构模板, 尚不能高效处理种类繁多的子结构, 特别是非环结构。据此, 本研究对分子结构式的多样性和内在特性进行了深入的分析, 提出一种子图塌缩的方法, 该方法可有效简化大图描述, 能够根据结构式的特点并结合子图匹配与频繁子图挖掘等方法对大图进行多级塌缩, 使得分子的匹配计算在多维度信息支持下变得可行, 进而有效地提高了分子识别与检索的准确率。

1 资料与方法

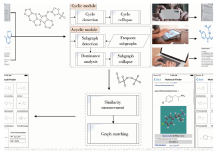
本文针对药物分子结构式的特点, 建立了一个完整的药物分子检索系统, 其框架如图1所示, 主要模块包括:多种模态的分子结构式查询输入(文本、图片、手绘图)、底层图形信息检测与中层图形特征提取及描述、图空间结构与拓扑关系分析、基于图密度与子图占优性分析的多级塌缩、超图构造、图匹配与相似性度量。

	Figure Option View Download New Window
	图1 基于图相似度的医药信息检索系统示意图Figure 1 Workflow of CSF retrieval system

1.1 输入与形式化

在本文方法中, 化学分子结构式可通过多种不同方式输入至检索系统。对于利用智能手机拍照的方式, 本文采用了一种规则化的方法从文本、图片和手绘图中提取分子结构式, 包括图像预处理、边缘检测、符号识别、结构式重建等关键技术。对于通过平板电脑手绘的方式, 本文针对性地采用了一些技术, 例如根据对时间序列的分析检测拐点、结合交互手势区别符号和线段、利用先验化学知识重建布局等。

结构式可表示为无向属性图, 其中顶点表示原子, 顶点间的边表示原子间的键。

定义1: 一个化学分子结构式定义为一个无向属性简单图 $G = (V, E, Ψ_{V}, Ψ_{E}, Γ_{V}, Γ_{E})$ 。

$V$ 为顶点集合, $E \subseteq V \times V$ 为边集合; $Ψ_{V}$ 和 $Ψ_{E}$ 作为标记函数, 分别为顶点和边分配属性; $Γ_{V}$ 和 $Γ_{E}$ 分别为顶点和边的属性集合。

采用无向图来表示结构式是一种沿用多年的常规表达方式, 但其所得到的图结构会面临一个重要的挑战, 即在原子数量增多后, 相应图的计算复杂度会呈指数级增加, 因此, 为提升检索效率, 本文针对结构式的特点探索大图简化的途径, 根据一个分子是否包含环状结构将其分为有环分子和无环分子两类, 分别进行处理。

1.2 环图塌缩

环状结构是结构式中的重要常见结构, 其具有相对稳定的化学性质, 采用有效方式对其进行塌缩可以简化分子的描述。这里的环状结构是指:每个顶点分别通过一条边和两个其他顶点相连, 即每个顶点的度数为2。要采用塌缩算法必须实现准确的环结构检测方法:对于任意给定的一个分子图结构, 使用RDKit^[15]方法提取其中的环结构; 将每个环塌缩为一个超级顶点, 并将其特征赋予到顶点属性中。同时, 为了准确描述该图中多个环结构之间的拓扑关系(如常见的相离、相切、相交、多重相交等空间位置关系), 本文构建了对应的环图 $G_{c}$ , 即在塌缩后的超级顶点之间建立边, 并通过细化边的属性记录原有环结构之间的空间关系。

1.3 无环图塌缩

不同于有环分子具有典型的环结构, 无环分子的子结构富有多样性, 为此需要借助更高层面的统计规律。例如, 对于给定的图数据集, 利用频繁子图挖掘技术检测具有代表性的非环结构, 由于候选非环子图之间存在多重选择性, 需要对其交叠情况进行更加细致的分析。为便于后文对上述方法进行详细介绍, 在此给出频繁子图的定义。

定义2:将一个频繁子图表示为具有支持度H(G_f)的图 $G_{f} = (V_{f}, E_{f}, Ψ_{V_{f}}, Ψ_{E_{f}}, Γ_{V_{f}}, Γ_{E_{f}})$ 。

$V_{f}$ 为顶点集合, $E_{f} \subseteq V_{f} \times V_{f}$ 为边集合; $Ψ_{V_{f}}$ 和 $Ψ_{E_{f}}$ 作为标记函数, 分别为顶点和边分配属性; $Γ_{V_{f}}$ 和 $Γ_{E_{f}}$ 分别为顶点和边的属性集合; $ε_{\min} \leq |V_{f}| \leq ε_{\max}$ ; 支持度H(G_f)定义了给定的图数据集中包含G_f的图的数量, H(G_f)≥ δ 。

1.3.1 基于频繁子图挖掘的非环结构筛选与环状结构稳定的布局特征不同, 大多数无环分子中的子结构不仅数量众多, 而且结构各异, 相互之间的空间布局关系也远比环状结构之间复杂, 较难进行统一描述。但很多非环子结构在大规模分子库中能呈现出一些统计特征, 因此, 本文利用频繁子图挖掘技术对其进行检测和筛选。具体来讲, 为检测一个给定的图数据集 $D = {G_{1}, G_{2}, \dots, G_{i}, \dots, G_{n}}$ 中的频繁子图, 可以为每个图G_i根据其字典序分配一个唯一的最小深度优先搜索(depth-first search, DFS)编码, 其由一种基于模式增长的方法gSpan^[16]确定。针对结构式的特点, 在子图挖掘过程中结合了具有一定化学性质的子结构(如官能团等)以提高所选择频繁子图的代表性。挖掘得到的频繁子图组成一个新的图集 $S_{f} = {G_{f}^{1}, G_{f}^{2}, \dots, G_{f}^{j}, \dots, G_{f}^{m}}$ , $j \leq m$ , 其中 $G_{f}^{j}$ 表示第 $j$ 个频繁子图, $m$ 表示频繁子图的总数。依据频繁子图, 可将每个图G_i∈ D表示为特征向量, $Λ_{i} = [λ_{i}^{G_{f}^{1}}, λ_{i}^{G_{f}^{2}}, \dots, λ_{i}^{G_{f}^{j}}, \dots, λ_{i}^{G_{f}^{m}}]$ , 其中 $λ_{i}^{G_{f}^{j}}$ 表示 $G_{f}^{j}$ 在 $G_{i}$ 存在的个数。

1.3.2 基于交叠子图覆盖最优化的非环结构塌缩在以塌缩方式处理非环子图结构之前, 还有一个重要的障碍需要克服, 即非环子图之间的重叠问题。由于可用于塌缩的候选非环子图有多种选择, 它们之间存在着相交(两个子图某些部分重叠)或包含(一个子图完全位于另一个子图内部)等交叠现象, 甚至同一类型的子图在同一分子结构图中也会出现多次且会互相重叠( $λ_{i}^{G_{f}^{j}} > 1$ )。不同的选择将会导致不同的塌缩结果, 进而生成不同的超图。本研究希望能够构建最小的超图, 使得后续的检索匹配代价最低, 为此需要在分析各种交叠可能性的基础上寻找最佳的非环子图组合方案。在算法设计中, 本文将寻找非环子图组合方案的问题转换为“ 最优子图覆盖” 问题, 即给定一个图和一组子图, 当挑选其中一些子图满足以下两个条件时, 这些子图构成对该图的一个最优覆盖:(1)两两之间不存在交叠; (2)在所有挑选方案中对该图的覆盖面积最大。然而, “ 枚举所有覆盖情况, 选择覆盖范围最大的集合” 是一个已知的NP-hard问题。于是, 本研究提出了一种基于占优子图的启发式算法(表1), 基于每个频繁子图 $G_{f}^{j}$ 的规模 $|V_{f}^{j}|$ 和支持度 $H (G_{f}^{j})$ 定义其占优度 $ω$ :

$ω (G_{f}^{j}) = |V_{f}^{j}| + H (G_{f}^{j}) / \overset{m}{\sum_{j = 1}} H (G_{f}^{j})$ (1)

$\begin{array}{l} H (G_{f}^{j}) = \overset{n}{\sum_{i = 1}} h (G_{f}^{j}, G_{i}), h (G_{f}^{j}, G_{i}) \\ = \{\begin{array}{l} 1, & λ_{i}^{G_{f}^{j}} \geq 1 \\ 0, & Otherwise . \end{array} \end{array}$ (2)

$Ω = {ω (G_{f}^{1}), ω (G_{f}^{2}), \dots, ω (G_{f}^{j}), \dots, ω (G_{f}^{m})}$ (3)

表1 占优子图挑选的算法 Table 1 Dominant subgraph selection

输入:G_i=(V_i, E_i,

Ψ_{V_{i}}

Ψ_{E_{i}}

Γ_{V_{i}}

Γ_{E_{i}}

)∈ D,
S_f={

G_{f}^{1}

G_{f}^{2}

, …,

G_{f}^{j}

, …,

G_{f}^{m}

}
Λ _i=

[λ_{i}^{G_{f}^{1}}, λ_{i}^{G_{f}^{2}}, \dots, λ_{i}^{G_{f}^{j}}, \dots, λ_{i}^{G_{f}^{m}}]

Ω = {ω (G_{f}^{1}), ω (G_{f}^{2}), \dots, ω (G_{f}^{j}), \dots, ω (G_{f}^{m})}

输出:

G_{i}

中占优子图
1:初始化

V_{i}

中所有顶点为未覆盖状态;
2:过滤

S_{f}

:保留在

G_{i}

中存在的频繁子图(

λ_{i}^{G_{f}^{j}}

≠ 0)作为候选集

S_{f}^{can}

;
3:将

S_{f}^{can}

中频繁子图依据其在

Ω

占优度降序排列;
4:初始化

S_{f}^{dom} = ϕ

S_{f}^{cov} = ϕ

;
5:对每个频繁子图

G_{f}^{x} \in S_{f}^{can}

6: 利用VF2算法在

G_{i}

中定位

G_{f}^{x}

的位置

γ (G_{f}^{x}, G_{i})

;
7: 对

G_{f}^{x}

在

G_{i}

中每个出现位置, 即

{G_{f}^{x}}_{y} \in γ (G_{f}^{x}, G_{i})

8: 如果

{G_{f}^{x}}_{y}

中所有顶点均未被覆盖, 则
9: 标记这些顶点为覆盖状态;
10: 将

{G_{f}^{x}}_{y}

添加至

S_{f}^{cov}

中;
11: 如果

G_{f}^{x}

不在

S_{f}^{dom}

中, 则
12: 将

G_{f}^{x}

添加至

S_{f}^{dom}

中;
13: 否则
14: 跳过

{G_{f}^{x}}_{y}

;

表1 占优子图挑选的算法 Table 1 Dominant subgraph selection

占优度 $[\forall ω (G_{f}^{j}) \in Ω]$ 既在局部特征方面考虑到频繁子图的规模显著程度, 同时又在分子库的全局范围考虑该频繁子图的频数在整个分子库的影响力, 据此设计的启发式算法可在多项式时间内找到满意解。具体算法(如表1所示):首先, 针对给定图 $G_{i}$ 将其所有顶点初始化为未覆盖状态; 其次, 在步骤2~3将该图包含的频繁子图( $λ_{i}^{G_{f}^{j}} \neq 0$ )作为候选集 $S_{f}^{can}$ , 并依据这些子图在 $Ω$ 中的占优度降序排序; 再次, 依次遍历这些频繁子图, 针对每次迭代中的最占优子图(占优度最高) $G_{f}^{x}$ , 通过子图同构算法VF2^[17]定位其在图 $G_{i}$ 出现的所有位置 $γ (G_{f}^{x}, G_{i})$ (步骤6); 最后, 在步骤7~14中, 检查 $G_{f}^{x}$ 的每个出现位置 ${G_{f}^{x}}_{y}$ [ ${G_{f}^{x}}_{y} \in γ (G_{f}^{x}, G_{i})]$ 对图 $G_{i}$ 的覆盖情况(步骤8), 如果 ${G_{f}^{x}}_{y}$ 包含的顶点均未被覆盖, 则在 $G_{i}$ 中标记这些顶点为覆盖状态, 并将 ${G_{f}^{x}}_{y}$ 的覆盖范围保存在 $S_{f}^{cov}$ ( $S_{f}^{cov}$ 用于标记占优子图在 $G_{i}$ 中的覆盖范围), 将当前迭代的子图 $G_{f}^{x}$ 保存在 $S_{f}^{dom}$ (如果还未包含在 $S_{f}^{dom}$ 中, $S_{f}^{dom}$ 用于存储 $G_{i}$ 的占优子图)(步骤9~12), 否则, 跳过当前出现位置 ${G_{f}^{x}}_{y}$ , 继续处理 $γ (G_{f}^{x}, G_{i})$ 中下一个出现位置 ${G_{f}^{x}}_{y + 1}$ 。通过多次迭代, 遍历了图 $G_{i}$ 包含的所有频繁子图, 最终得到最优覆盖集合。

1.4 超图构造

为统一表示塌缩后的结构式, 需要引入更具抽象度高层图结构描述方法— — 超图。

定义3:基于化学分子结构式原图 $G = (V, E, Ψ_{V}, Ψ_{E}, Γ_{V}, Γ_{E})$ 定义超图 $G_{h} = (V_{h}, E_{h}, Ψ_{V_{h}}, Ψ_{E_{h}}, Γ_{V_{h}}, Γ_{E_{h}})$ 。

$V_{h}$ 为超顶点集合, 一个超顶点包含至少一个原顶点( $v \in V$ ), $E_{h} \subseteq V_{h} \times V_{h}$ 为超边集合; $Ψ_{V_{h}}$ 和 $Ψ_{E_{h}}$ 作为标记函数, 分别为超顶点和超边分配属性; $Γ_{V_{h}}$ 和 $Γ_{E_{h}}$ 分别为顶点和边的属性集合。

对于有环分子, 以其环图 $G_{c}$ 为基础构建超图G_h。定义 $V_{ac}$ 和 $E_{ac}$ 分别包含原图中所有不属于环的顶点和边, 以 $G_{c}$ 初始化超图 $G_{h}$ , 将 $V_{ac}$ 中顶点依次添加至超图 $G_{h}$ 。判定 $E_{ac}$ 中每条边是否连接到原图中任何环, 如果某条边连接至一个环, 则在超图 $G_{h}$ 中插入一条相应的超边, 其连接两个超顶点, 分别表示原图中该边连接的非环顶点和环, $E_{ac}$ 中剩余不连接任何环的边也被依次添加至超图 $G_{h}$ , 最终生成相应超图。

对于无环分子, 依据表1算法所得占优子图结果, 将 $S_{f}^{cov}$ 中占优子图覆盖的范围塌缩为超图 $G_{h}$ 中相应超顶点, 剩余原图中未被覆盖的顶点依次添加至 $G_{h}$ 。检查原图中未被覆盖的每条边是否连接 $S_{f}^{cov}$ 中任何子图, 如果某条边连接至一个或两个被覆盖子图, 则向超图 $G_{h}$ 插入一条边, 连接两个超顶点, 表示原图中两个相邻子图(即一个被覆盖子图和一个未被覆盖顶点, 或者两个被覆盖子图)。将原图中剩余未被覆盖的边依次添加至超图, 得到最终的超图。

1.5 相似性度量

结构式的相似度度量是实现检索目标的最后一步。本文采用了分级匹配的策略:对于一个查询分子, 先计算其与数据集中其他分子在超图级别的最小图编辑距离, 进行初筛, 得到一个候选分子集合, 再在原图级别计算查询分子与候选集中其他分子的最小图编辑距离及其子图同构的数量, 综合评价两者的相似度, 得到更为精确的检索结果。

2 结果与讨论

基于本系统的实验性检索网站为www.pharmki.com。为了评估本系统的检索准确率, 我们将其和维基化学结构检索系统(Wikipedia Chemical Structure Explorer, WCSE)^[18]进行了对比, 并通过一些具体的检索实例进一步和WCSE进行直观比较。

本研究实验环境如下:一台配置为3.2 GHz Intel Core i5处理器和16G内存的iMac, 代码由MATLAB R2016b编译。采用的数据集为Wikipedia分子数据集(下文简称为WIKI, 网址为:http://www.cheminfo.org/wikipedia/smiles.txt), 该数据集共有14 676个分子, 每个分子的平均原子数量为41.41, 最大为1 262, 最小为1, 每个分子的平均键数量为42.48, 最大为1 338, 最小为0。

定义2中的参数 $ε_{\min} = 3$ , $ε_{\max} = 300$ , 用于在WIKI数据集中挖掘频繁子图。为了设定合适的参数 $δ$ (子图频率), 本文统计了不同 $δ$ 值下从WIKI数据集中得到的频繁子图的数量, 其结果显示, 频繁子图的数量在 $δ$ 大于10%后变化不大, 所以设定 $δ = 10 %$ 。

WCSE是目前在已公开完整数据集的化学分子结构式检索系统中检索效果最好的, 其所用WIKI数据集可用于对比实验。本文系统与WCSE的对比结果如表2所示, 其中, mean average precision(MAP)、discounted cumulative gain (DCG)、rank-biased precision(RBP)和expected reciprocal rank(ERR)是衡量检索准确性的指标, RBP指标的参数p设定为0.85, 设定检索结果范围为前2~10个, 即表2中top-2到top-10。结果显示, 本文系统在各项指标度量均比WCSE表现更好, 例如, 针对top-10, 上述指标的领先幅度分别为10%、1.41、6.42%、1.32%。具体而言, MAP指标表明本文系统比WCSE能检索到更多的相似结构式; 更高的DCG数值则说明其对结果中的相似结构式排序效果更好。此外, 本文系统在RBP85和ERR指标的更好表现, 则进一步说明其返回的相似结构式结果相比WCSE更符合用户的查询意图。观察表2中各项指标随top-k变化的趋势, 可以发现两者在MAP指标上的表现均逐渐走低, 表明两个系统均倾向于将更相似的结构式优先返回。两者ERR数值趋于稳定, 说明两个系统均能返回满意度较高的结果。但对于DCG和RBP85两个指标, 两系统的差距均逐渐加大, 这表明本文系统在更大范围的检索上表现更优。综上所述, 本文方法不仅能检索到更多相似的分子结构式, 而且检索结果有更好的排序效果, 即优先返回更相似的分子结构式。

表2 top-k(2~10)检索结果的MAP(%)、DCG、RBP85(%)、ERR(%)值 Table 2 MAP(%), DCG, RBP85(%), and ERR(%) at

top⁃k

(2-10) results

Metric	Ours	WCSE	Metric	Ours	WCSE	Metric	Ours	WCSE	Metric	Ours	WCSE
MAP₂	96.00	91.50	DCG₂	18.12	17.38	RBP85₂	26.73	25.58	ERR₂	94.60	93.20
MAP₃	89.67	84.33	DCG₃	19.67	18.82	RBP85₃	35.07	33.17	ERR₃	94.84	93.49
MAP₄	85.13	79.88	DCG₄	20.71	19.78	RBP85₄	41.66	39.29	ERR₄	94.94	93.61
MAP₅	82.20	76.90	DCG₅	21.58	20.50	RBP85₅	47.18	44.38	ERR₅	95.00	93.67
MAP₆	79.50	73.25	DCG₆	22.59	21.11	RBP85₆	51.57	48.04	ERR₆	95.03	93.71
MAP₇	77.07	69.50	DCG₇	22.82	21.58	RBP85₇	55.11	50.70	ERR₇	95.05	93.73
MAP₈	74.94	66.69	DCG₈	23.25	22.03	RBP85₈	58.00	52.96	ERR₈	95.06	93.75
MAP₉	72.61	63.00	DCG₉	23.65	22.29	RBP85₉	60.20	54.33	ERR₉	95.08	93.75
MAP₁₀	70.45	60.20	DCG₁₀	23.96	22.55	RBP85₁₀	61.97	55.55	ERR₁₀	95.08	93.76

WCSE, Wikipedia Chemical Structure Explorer; MAP, mean average precision; DCG, discounted cumulative gain; RBP, rank-biased precision; ERR, expected reciprocal rank.

表2 top-k(2~10)检索结果的MAP(%)、DCG、RBP85(%)、ERR(%)值 Table 2 MAP(%), DCG, RBP85(%), and ERR(%) at

top⁃k

(2-10) results

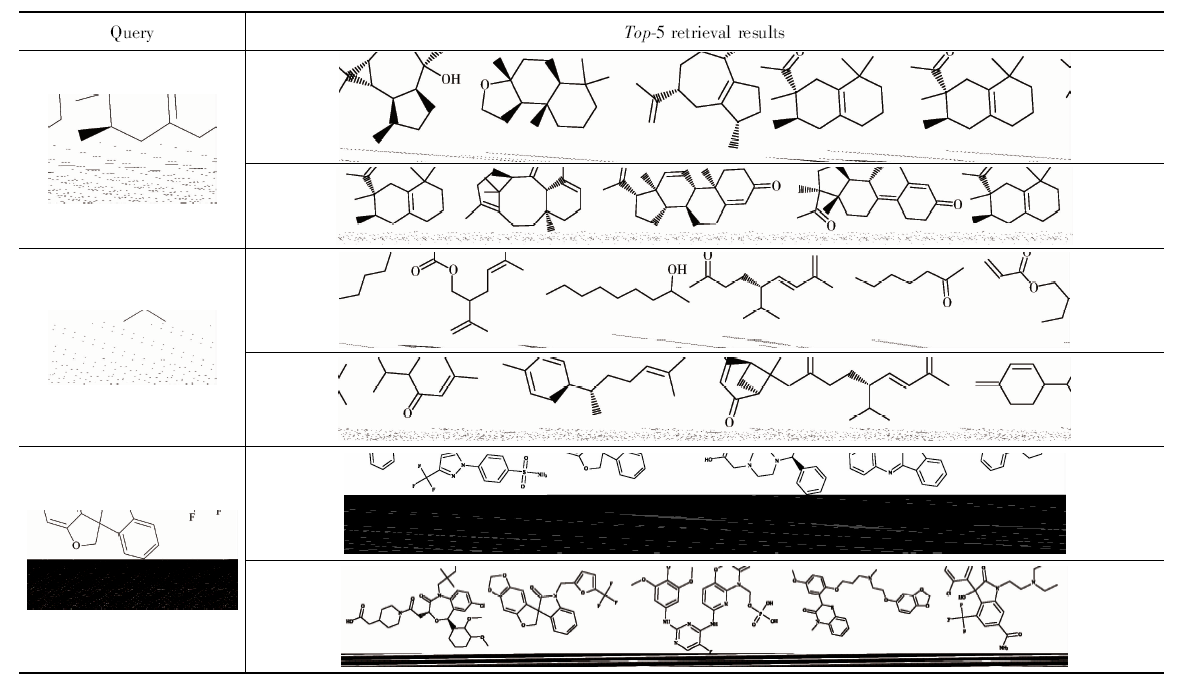
为更直观地比较本文系统和WCSE, 表3展示了一些查询实例及其在两个系统上的检索结果, 设定的检索结果范围为前5个。可见两个系统均能将精确匹配的结果作为第一个候选项返回, 但是在剩余的候选结果中则存在着明显差异。第一个查询分子龙涎酮主要由两个环构成, 本文系统返回了3个同样具有两个环的相似分子, 而WCSE只返回了1个具有两个环的分子, 其余结果和龙涎酮并不相似。第二个查询分子茄酮为无环分子, 主要结构为5-丙基-8-甲基-二烯酮, 本文系统的检索结果均为包含碳链的类似茄酮的无环分子, 而WCSE的返回结果却都是有环分子。第三个查询分子Funapide包含6个环和1个三氟甲基, 本检索系统返回的4个结果均包含1个三氟甲基, 且具有3个或者4个环, 而WCSE的检索结果中只有1个分子具有三氟甲基。

表3 WIKI数据集中top-5检索结果对比:本文与WCSE Table 3 Comparison of the top-5 retrieval results from the proposed method and WCSE on WIKI

针对备受关注的医药信息检索, 结合化学分子结构式的丰富空间结构信息和表征化合物的唯一性, 本文提出了一种基于图结构相似度的分子结构式检索方法。该方法通过智能终端的拍照或手绘实现输入结构式, 以子图匹配和频繁子图挖掘等方法为基础, 结合结构式的结构特性对大图进行多级塌缩, 得到相应的高级抽象表示— — 超图, 其在筛选子图的关键环节采用了基于图同构的子图覆盖分析方法, 并采用不同粒度信息(图编辑距离和子图同构等)实现精确的分子匹配。实验结果显示, 本文方法不仅在多项检索准确率指标均具有优势, 而且直观效果更佳, 表明此方法针对药物分子检索更具有效性, 能为用户提供更为满意的分子检索结果。当然, 在该研究方向上还有许多问题值得进一步探索, 例如, 如何构建大分子的多层级超图、如何设计能够传递三维信息的立体图, 以及如何实现更高效的图匹配等。

The authors have declared that no competing interests exist.

参考文献

文献选项

[1]	Weininger D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules[J]. Journal of Chemical Information & Computer Sciences, 1988, 28(1): 31-36. [本文引用:1]
[2]	Muegge I, Mukherjee P. An overview of molecular fingerprint si-milarity search in virtual screening[J]. Expert Opin Drug Discov, 2016, 11(2): 137-148. [本文引用:1]
[3]	Taitz Y, Weiniger D, Delany J. Daylight[CP/OL]. California, USA: Daylight Chemical Information Systems, Inc. Laguna Niguel. http://www.daylight.com. [本文引用:1]
[4]	Pan S, Zhu X. Graph classification with imbalanced class distributions and noise[C]//Proceedings of the twenty-third international joint conference on artificial intelligence. Washington, USA: AAAI Press, 2013: 1586-1592. [本文引用:1]
[5]	Kier LB, Hall LH. Molecular structure description[J]. Pigment Cell & Melanoma Research, 1999, 3(S2): 61-66. [本文引用:1]
[6]	Gálvez J, García-Domenech R, Julian-Ortiz JVD, et al. Topological approach to drug design[J]. J Chemical Information & Computer Sciences, 1995, 35(2): 272-284. [本文引用:1]
[7]	Abu ElAtta AH, Moussa MI, Hassanien AE. Predicting activity approach based on new atoms similarity kernel function[J]. J Mol Graph Model, 2015, 60: 55-62. [本文引用:1]
[8]	Raymond JW, Willett P. Maximum common subgraph isomorphism algorithms for the matching of chemical structures[J]. J Comput Aided Mol Des, 2002, 16(7): 521-533. [本文引用:1]
[9]	Deshpand e M, Kuramochi M, Wale N, et al. Frequent substructure-based approaches for classifying chemical compounds[J]. IEEE Trans Knowl Data Eng, 2005, 17(8): 1036-1050. [本文引用:1]
[10]	Riesen K, Bunke H. Approximate graph edit distance computation by means of bipartite graph matching[J]. Image Vis Comput, 2009, 27(7): 950-959. [本文引用:1]
[11]	Jouili S, Tabbone S. Graph embedding using constant shift embedding[C]// Proceedings of the twentieth international conference on recognizing patterns in signals, speech, images, and videos. Istanbul, Turkey: Springer-Verlag, 2010: 83-92. [本文引用:1]
[12]	Gibert J, Valveny E, Bunke H. Graph embedding in vector spaces by node attribute statistics[J]. Pattern Recognit, 2012, 45(9): 3072-3083. [本文引用:1]
[13]	Gaüzère B, Brun L, Villemin D. Two new graphs kernels in chemoinformatics[J]. Pattern Recognit Lett, 2012, 33(15): 2038-2047. [本文引用:1]
[14]	Horváth T, Gartner T, Wrobel S. Cyclic pattern kernels for predictive graph mining[C]//Proceedings of the tenth ACM SIGKDD international conference on knowledge discovery and data mining. Seattle, USA: ACM, 2004: 158-167. [本文引用:1]
[15]	Land rum G. RDKit: open-source cheminformatics [CP/OL]. http://www.rdkit.org. [本文引用:1]
[16]	Yan X, Han J. Gspan: graph-based substructure pattern mining[C]//Proceedings of the 2002 IEEE international conference on data mining. Maebashi, Japan: IEEE Computer Society, 2002: 721-724. [本文引用:1]
[17]	Cordella LP, Foggia P, Sansone C, et al. A (sub)graph isomorphism algorithm for matching large graphs[J]. IEEE Trans Pattern Anal Mach Intell, 2004, 26(10): 1367-1372. [本文引用:1]
[18]	Ertl P, Patiny L, Sand er T, et al. Wikipedia chemical structure explorer: substructure and similarity searching of molecules from Wikipedia[J]. J Cheminform, 2015, 7(1): 10. [本文引用:1]

1988

0.0

... 许多生物和化学信息用连续字符串来表示分子,如最具代表性的SMILES(Simplified Molecular Input Line Entry System)^[1]语言,但此类编码方法忽略过多的结构信息 ...

2016

0.0

... 分子指纹^[2]是另一类简单的分子编码方式,如拓扑指纹(topological fingerprints)^[3]将代表分子特征的键径转换为给定数量的连接键,但分子指纹在精确描述空间结构方面仍有一些困难 ...

0.0

2013

0.0

... 图是在化学信息学和生物信息学领域中被广泛应用的一种通用的数据结构^[4],但当分子结构式随着原子数增加变成大图后,该方法会因计算代价的瓶颈而无法取得很好的实用性 ...

1999

0.0

... 图描述符涉及的范围较广,包括从一维的统计^[5]到二维的拓扑指数^[6],再到复杂的三维描述^[7] ...

1995

0.0

... 图描述符涉及的范围较广,包括从一维的统计^[5]到二维的拓扑指数^[6],再到复杂的三维描述^[7] ...

2015

0.0

... 图描述符涉及的范围较广,包括从一维的统计^[5]到二维的拓扑指数^[6],再到复杂的三维描述^[7] ...

2002

0.0

... 图挖掘旨在研究相似的化合物或者预测分子的物化和生物性质,所应用的常规技术包括最大公共子图^[8]、频繁子图挖掘^[9]和编辑距离^[10] ...

2005

0.0

... 图挖掘旨在研究相似的化合物或者预测分子的物化和生物性质,所应用的常规技术包括最大公共子图^[8]、频繁子图挖掘^[9]和编辑距离^[10] ...

2009

0.0

... 图挖掘旨在研究相似的化合物或者预测分子的物化和生物性质,所应用的常规技术包括最大公共子图^[8]、频繁子图挖掘^[9]和编辑距离^[10] ...

2010

0.0

... 为了将图与机器学习方法相结合,需要将每一个图映射到一个显式的向量空间^[11] ...

2012

0.0

... 在新的向量空间中,被嵌入图通过所获编码进行差异比较^[12],从而度量出属性的统计特征 ...

2012

0.0

... re等^[13]采用了由严格子树集定义的模式袋(bag of pattern),即所有具有最多六个节点的标签树的集合 ...

2004

0.0

... 环模式核(cyclic pattern kernel)^[14]把一个图分解成一个具有环结构的集合和一个与不在环中的原子和边相对应的集合 ...

0.0

... 要采用塌缩算法必须实现准确的环结构检测方法:对于任意给定的一个分子图结构,使用RDKit^[15]方法提取其中的环结构 ...

2002

0.0

... 具体来讲,为检测一个给定的图数据集 D={G1,G2,…,Gi,…,Gn}中的频繁子图,可以为每个图G_i根据其字典序分配一个唯一的最小深度优先搜索(depth-first search,DFS)编码,其由一种基于模式增长的方法gSpan^[16]确定 ...

2004

0.0

... 再次,依次遍历这些频繁子图,针对每次迭代中的最占优子图(占优度最高) Gfx,通过子图同构算法VF2^[17]定位其在图 Gi出现的所有位置 γ(Gfx,Gi)(步骤6) ...

2015

0.0

... 为了评估本系统的检索准确率,我们将其和维基化学结构检索系统(Wikipedia Chemical Structure Explorer,WCSE)^[18]进行了对比,并通过一些具体的检索实例进一步和WCSE进行直观比较 ...