下颌骨颏部骨折联合双侧髁突囊内骨折致伤机制的三维有限元分析

doi:10.19723/j.issn.1671-167X.2021.05.029

摘要/Abstract

摘要：

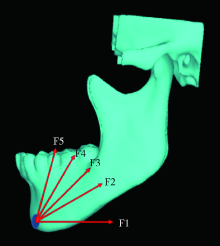
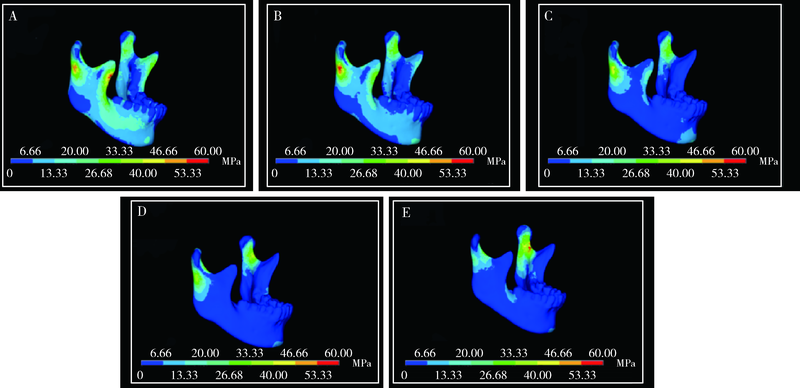
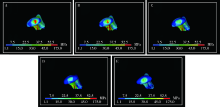
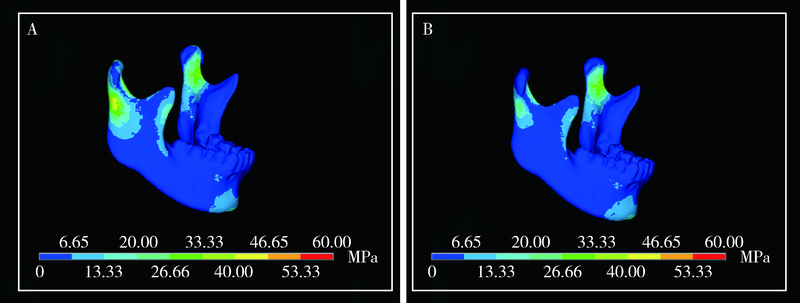
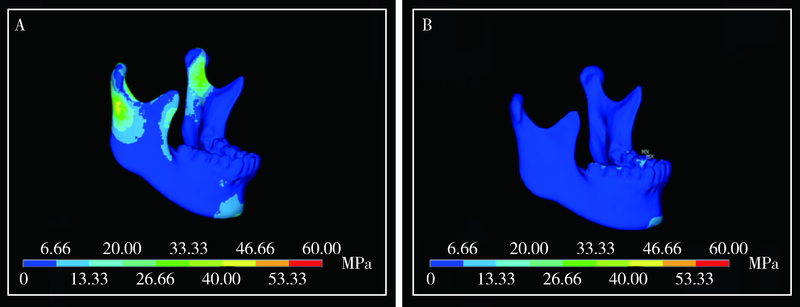
目的: 通过三维有限元方法模拟和分析下颌骨颏部骨折联合双侧髁突囊内骨折的致伤机制,提高此类骨折的预防和诊断水平。方法: 获取1名下颌骨发育正常、无第三磨牙、无颞下颌关节病史的青年男性的颌面部CT和颞下颌关节MRI数据,通过Mimics和ANSYS软件建立三维有限元模型。采取不同角度的外力作用于下颌骨颏部,分析下颌骨及髁突关节面的应力分布。同时,比较有无关节盘、咬合与非咬合状态下下颌骨的应力分布差异。结果: 准确建立了包含颞下颌关节结构的三维有限元模型。当外力作用于下颌骨颏部时,髁突、升支前缘及颏部受力区是主要的应力集中区,其中应力最大值位于髁突顶部。随着外力方向与水平面夹角由0°逐渐增大直至60°,下颌骨上的应力由分散逐渐集中至颏部与双侧髁突三个部位;超过60°时,应力又出现分散的趋势。当对关节盘进行模拟后,髁突关节面及髁颈部的应力分布明显减小。与非咬合状态相比,咬合状态下下颌骨上的应力集中于咬合面,而其他部位无明显的应力分布。结论: 外力方向与水平面呈60°时,应力分布主要集中于颏部及双侧髁突顶部,即三点骨折发生的部位;在下颌骨颏部受力过程中,关节盘的存在以及稳定的咬合状态下,髁突部位(包括颈部和关节面)的应力分布明显减小。

关键词: 颏部骨折, 髁突囊内骨折, 下颌骨, 有限元分析

Abstract:

Objective: To analyze the biomechanical mechanism of mandibular symphyseal fracture combined with bilateral intracapsular condylar fractures using finite element analysis (FEA). Methods: Maxillofacial CT scans and temporomandibular joint (TMJ) MRI were performed on a young male with normal mandible, no wisdom teeth and no history of TMJ diseases. The three-dimensional finite element model of mandible was established by Mimics and ANSYS based on the CT and MRI data. The stress distributions of mandible with different angles of traumatic loads applied on the symphyseal region were analyzed. Besides, two models with or without disc, two working conditions in occlusal or non-occlusal status were established, respectively, and the differences of stress distribution between them were compared. Results: A three-dimensional finite element model of mandible including TMJ was established successfully with the geometry and mechanical properties to reproduce a normal mandibular structure. Following a blow to the mandibular symphysis with different angles, stress concentration areas were mainly located at condyle, anterior border of ramus and symphyseal region under all conditions. The maximum equivalent stress always appeared on condylar articular surface. As the angle between the external force and the horizontal plane gradually increased from 0° to 60°, the stress on the mandible gradually concentrated to symphysis and bilateral condyle. However, when the angle between the external force and the horizontal plane exceeded 60°, the stress tended to disperse to other parts of the mandible. Compared with the condition without simulating the disc, the stress distribution of articular surface and condylar neck decreased significantly when the disc was present. Compared with non-occlusal status, the stress on the mandible in occlusal status mainly distributed on the occlusal surface, and no stress concentration was found in other parts of the mandible. Conclusion: When the direction of external force is 60° from the horizontal plane, the stress distribution mainly concentrates on symphyseal region and bilateral condylar surface, which explains the occurrence of symphyseal fracture and intracapsular condylar fracture. The stress distribution of condyle (including articular surface and condylar neck) decreases significantly in the presence of arti-cular disc and in stable occlusal status when mandibular symphysis is under traumatic force.

Key words: Symphyseal fracture, Intracapsular condylar fracture, Mandible, Finite element analysis

中图分类号:

R782.6

周伟,安金刚,荣起国,张益. 下颌骨颏部骨折联合双侧髁突囊内骨折致伤机制的三维有限元分析[J]. 北京大学学报（医学版）, 2021, 53(5): 983-989.

Wei ZHOU,Jin-gang AN,Qi-guo RONG,Yi ZHANG. Three-dimensional finite element analysis of traumatic mechanism of mandibular symphyseal fracture combined with bilateral intracapsular condylar fractures[J]. Journal of Peking University (Health Sciences), 2021, 53(5): 983-989.

图/表 9

图1

表1

表2

图2

图3

表3

图4

图5

图6

参考文献 19

[1]	武付花, 黄迪炎, 郭振国, 等. 三维有限元分析下颌骨不同部位受力髁突的力学应变 [J]. 中国组织工程研究, 2015, 19(29):4667-4671.
[2]	Gallas-Torreira M, Fernandez JR. A three-dimensional computer model of the human mandible in two simulated standard trauma situations [J]. J Craniomaxillofac Surg, 2004, 32(5):303-307. doi: 10.1016/j.jcms.2004.04.008
[3]	徐晓峰, 苏佳楠, 代杰文, 等. 颏部骨折合并双侧髁突囊内骨折3种不同治疗方式的三维有限元分析 [J]. 中国口腔颌面外科杂志, 2016, 14(5):409-412.
[4]	Liu YF, Wang R, Baur DA, et al. A finite element analysis of the stress distribution to the mandible from impact forces with various orientations of third molars [J]. J Zhejiang Univ Sci B, 2018, 19(1):38-48. doi: 10.1631/jzus.B1600552
[5]	Loukota RA, Neff A, Rasse M. Nomenclature/classification of fractures of the mandibular condylar head [J]. Br J Oral Maxillofac Surg, 2010, 48(6):477-478. doi: 10.1016/j.bjoms.2009.08.036 pmid: 19896755
[6]	Antic S, Vukicevic AM, Milasinovic M, et al. Impact of the lower third molar presence and position on the fragility of mandibular angle and condyle: A Three-dimensional finite element study [J]. J Craniomaxillofac Surg, 2015, 43(6):870-878. doi: 10.1016/j.jcms.2015.03.025
[7]	Thresher RW, Saito GE. The stress analysis of human teeth [J]. J Biomech, 1973, 6(5):443-449. pmid: 4748494
[8]	Arne W, Wolfgang K, Kurt S, et al. A 3-dimensional finite-element analysis investigating the biomechanical behavior of the mandible and plate osteosynjournal in cases of fractures of the condylar process [J]. Oral Surg Oral Med Oral Pathol Oral Radiol Endod, 2002, 94(6):678-686. doi: 10.1067/moe.2002.126451
[9]	Rho JY, Hobatho MC, Ashman RB. Relations of mechanical properties to density and CT numbers in human bone [J]. Med Eng Phys, 1995, 17(5):347-355. pmid: 7670694
[10]	Wang R, Liu Y, Wang JH, et al. Effect of interfragmentary gap on the mechanical behavior of mandibular angle fracture with three fixation designs: A finite element analysis [J]. J Plast Reconstr Aesthet Surg, 2017, 70(3):360-369. doi: 10.1016/j.bjps.2016.10.026
[11]	Chaudhry H, Bukiet B, Anderson EZ, et al. Muscle strength and stiffness in resistance exercise: Force transmission in tissues [J]. J Bodyw Mov Ther, 2017, 21(3):517-522. doi: S1360-8592(16)30128-0 pmid: 28750958
[12]	Weijs WA, Hillen B. Relationship between the physiological cross-section of the human jaw muscles and their cross-sectional area in computer tomograms [J]. Acta Anat, 1984, 121(1):31-35. doi: 10.1159/000145938
[13]	Bezerra TP, Silva Junior FI, Scarparo HC, et al. Do erupted third molars weaken the mandibular angle after trauma to the chin region? A 3D finite element study [J]. Int J Oral Maxillofac Surg, 2013, 42(4):474-480. doi: 10.1016/j.ijom.2012.10.009
[14]	Santos LS, Rossi AC, Freire AR, et al. Finite-element analysis of 3 situations of trauma in the human edentulous mandible [J]. J Oral Maxillofac Surg, 2015, 73(4):683-691. doi: 10.1016/j.joms.2014.10.014
[15]	Stringhini DJ, Sommerfeld R, Uetanabaro LC, et al. Resistance and stress finite element analysis of different types of fixation for mandibular orthognathic surgery [J]. Braz Dent J, 2016, 27(3):284-291. doi: 10.1590/0103-6440201600336 pmid: 27224561
[16]	Bujtar P, Sandor GK, Bojtos A, et al. Finite element analysis of the human mandible at 3 different stages of life [J]. Oral Surg Oral Med Oral Pathol Oral Radiol Endod, 2010, 110(3):301-309. doi: 10.1016/j.tripleo.2010.01.025
[17]	Sun M, Yang J, Zhou R, et al. Mechanical analysis on individualized finite element of temporal-mandibular joint under overlarge jaw opening status [J]. Int J Clin Exp Med, 2015, 8(6):9046.
[18]	Cheng HY, Peng PW, Lin YJ, et al. Stress analysis during jaw movement based on vivo computed tomography images from patients with temporomandibular disorders [J]. Int J Oral Maxillofac Surg, 2013, 42(3):386-392. doi: 10.1016/j.ijom.2012.07.005
[19]	Chen S, Zhang Y, An JG, et al. Width-controlling fixation of symphyseal/parasymphyseal fractures associated with bilateral condylar fractures with 22.0 mm miniplates: A retrospective investigation of 45 cases [J]. J Oral Maxillofac Surg, 2016, 74(2):315-327. doi: 10.1016/j.joms.2015.09.030

相关文章 15

[1]	马珂楠,陈虎,沈妍汝,周永胜,王勇,孙玉春. 选择性激光熔化打印可摘局部义齿圆环形卡环固位力的有限元分析[J]. 北京大学学报（医学版）, 2022, 54(1): 105-112.
[2]	任爽,时会娟,张家豪,刘振龙,邵嘉艺,朱敬先,胡晓青,黄红拾,敖英芳. 前交叉韧带重建术后移植物应力的有限元分析[J]. 北京大学学报（医学版）, 2021, 53(5): 865-870.
[3]	姜又升,冯琳,高学军. 垫底材料弹性模量对髓腔固位冠修复后上颌前磨牙应力分布的影响[J]. 北京大学学报（医学版）, 2021, 53(4): 764-769.
[4]	林春平,卢松鹤,朱浚鑫,胡洪成,岳兆国,唐志辉. 个性化根形种植体的螺纹形态对周围牙槽骨应力分布影响的三维有限元分析[J]. 北京大学学报（医学版）, 2019, 51(6): 1130-1137.
[5]	李博文,吴唯伊,唐琳,张一,刘玉华. 改良猪小肠黏膜下层可吸收膜在兔下颌骨缺损早期愈合中的作用[J]. 北京大学学报（医学版）, 2019, 51(5): 887-892.
[6]	付宏宇,王芳芳,侯晓玫. 控制记忆合金丝镍钛根管锉弯曲性能有限元分析模型的构建及力学分析[J]. 北京大学学报（医学版）, 2019, 51(1): 131-135.
[7]	李明哲,王晓霞,李自力,伊彪,梁成,何伟. 计算机导航辅助下口内入路髁突切除术精确性分析[J]. 北京大学学报（医学版）, 2019, 51(1): 182-186.
[8]	戴帆帆，刘怡，许天民，陈贵. 探索成人正畸前后下颌三维数字化模型的重叠方法[J]. 北京大学学报(医学版), 2018, 50(2): 271-278.
[9]	柳大为，李晶，郭亮，荣起国，周彦恒. 舌侧矫治器关闭间隙上前牙牙周膜应力变化的三维有限元分析[J]. 北京大学学报(医学版), 2018, 50(1): 141-147.
[10]	李世赢，李刚，冯海兰，潘韶霞. 锥形束CT分析下颌无牙颌患者前部颌弓形态对“All-on-4”种植设计的影响[J]. 北京大学学报(医学版), 2017, 49(4): 699-703.
[11]	孙丽颖，郭阳，荣起国，田光磊. 舟骨骨折术后康复治疗的有限元分析[J]. 北京大学学报(医学版), 2016, 48(4): 751-封三.
[12]	赵旭，张磊，孙健，杨振宇，谢秋菲. 后牙种植体支持单冠牙合面高度的三维有限元力学分析[J]. 北京大学学报(医学版), 2016, 48(1): 94-100.
[13]	甄敏，胡文杰，荣起国. 上颌中切牙冠根折行冠延长术并桩核冠修复的三维有限元分析[J]. 北京大学学报(医学版), 2015, 47(6): 1015-1021.
[14]	何伟，谢晓艳，王兴，王晓霞，傅开元，李自力. 上颌Le FortⅠ型分块截骨术及双侧下颌升支矢状劈开术对骨性Ⅲ类错牙合畸形患者髁突位置的影响[J]. 北京大学学报(医学版), 2015, 47(5): 829-833.
[15]	陈全, 郭传瑸, 高涛. 54例大致正常成年汉族人下颌骨三维CT形态学测量[J]. 北京大学学报（医学版）, 2015, 47(1): 113-119.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

Gray value/HU	Density/(kg/m³)	Young modulus/(MPa)	Poisson ratio
226.0-510.5	451.32	2 209.07	0.3
510.5-795.0	711.92	4 124.77
795.0-1 079.5	972.52	6 324.00
1 079.5-1 364.0	1 232.67	8 750.40
1 364.0-1 648.5	1 493.73	11 384.68
1 648.5-1 933.0	1 754.33	14 190.63
1 933.0-2 217.5	2 014.93	17 155.61
2 217.5-2 502.0	2 275.53	20 266.26
2 502.0-2 786.5	2 536.13	23 511.80
2 786.5-3 071.0	2 796.74	26 883.29

Muscle	Cross sectional area/cm²	Number of elements, n	Young modulus/MPa	Poisson ratio
Masseter	6.80	28	19	0.3
Medial pterygoid	4.37	18	19
Lateral pterygoid	2.39	9	19
Anterior temporal	4.12	17	19
Posterior temporal	4.12	17	19

Angle between load and horizontal plane/(°)	Symphysis/MPa	Anterior border of ramus/MPa	Condylar articular surface/MPa
0	25.2	67.4	174.6
30	24.5	43.5	137.3
45	21.1	23.0	64.8
60	19.8	7.3	56.3
75	16.4	17.9	54.6