个性化根形种植体的螺纹形态对周围牙槽骨应力分布影响的三维有限元分析

doi:10.19723/j.issn.1671-167X.2019.06.027

摘要/Abstract

摘要：

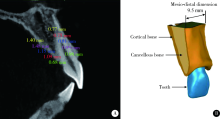
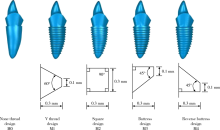
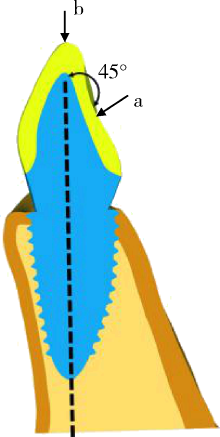
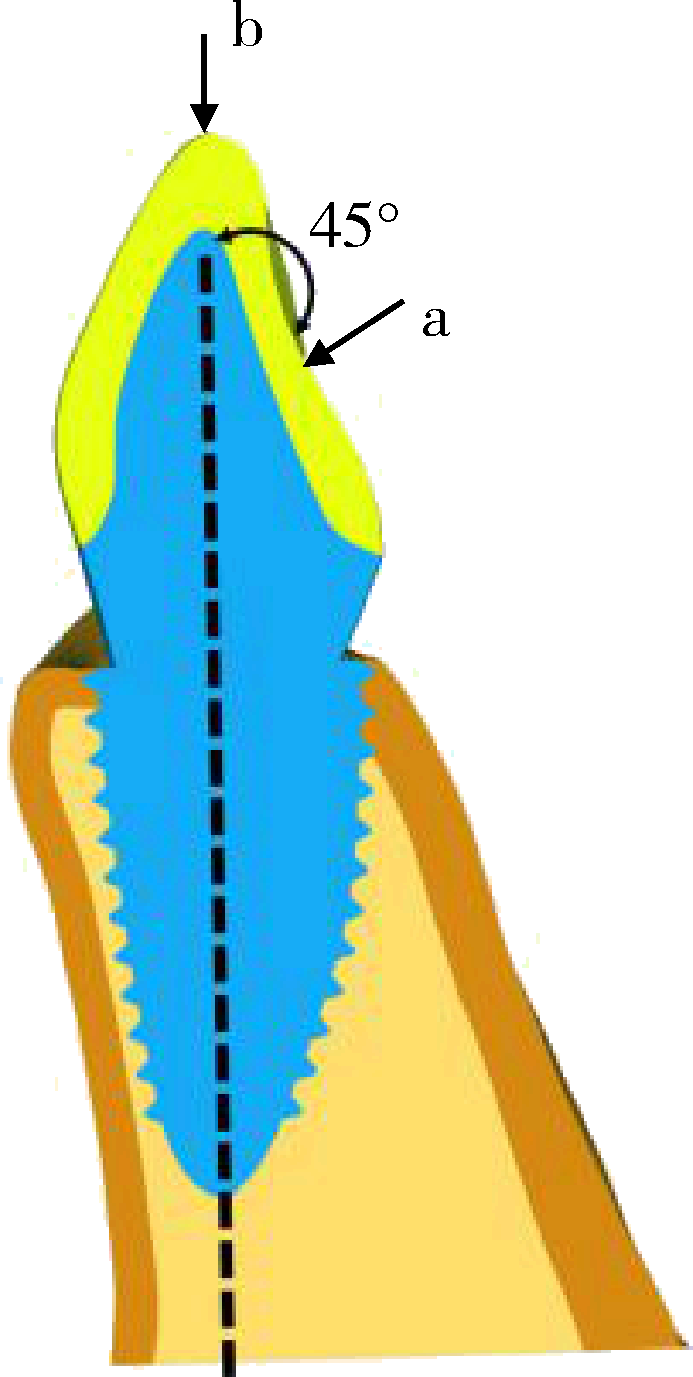
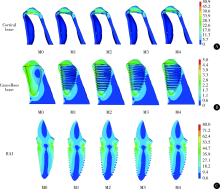
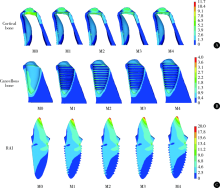
目的探讨个性化根形种植体的螺纹形态设计对周围牙槽骨应力分布的影响。方法通过逆向建模技术建立带有矩形、V形、支撑形、反支撑形螺纹和不带螺纹的一段式个性化根形牙种植体的三维有限元模型,分别加载与种植体长轴呈45°角及0°角的100 N的力,导入Ansys 16软件计算不同螺纹个性化根形种植体周围骨组织von Mises应力分布的情况。结果倾斜45°角加载时,皮质骨内应力主要集中于种植体颈部周缘及螺纹顶端,松质骨内应力主要分布于种植体唇侧颈部、螺纹顶端和植体根尖部。垂直(0°角)加载时,皮质骨内应力主要集中于种植体颈部处,松质骨内应力主要分布于根尖部以及唇侧根下部。加载时,螺纹组相对无螺纹组应力分布更加均匀,各螺纹组间无明显差别。松质骨内各螺纹植体应力主要集中在螺纹顶端处,根尖处的应力集中较少。与矩形螺纹相比,V形、支撑形和反支撑形种植体在松质骨内的应力分布更为均匀。结论螺纹设计可以优化个性化根形种植体周围皮质骨和松质骨内的应力分布,减小皮质骨内的应力集中,V形、支撑形、反支撑形相比矩形螺纹设计,应力分布更加均匀。

关键词: 种植体螺纹, 牙种植体, 有限元分析, 牙应力分析

Abstract:

Objective: To explore the effects from the thread shapes of custom-made root-analogue implant (RAI) on distributions of von Mises stress around the peri-implant bone.Methods: Five one-stage RAI three-dimensional finite element (FE) models with different thread shapes (V-shaped design, square design, buttress design, reverse buttress design and none thread design) and congruent bone were created through reverse engineering technology. The data of the five models were imported into the FE analysis software to calculate. A force of 100 N was applied parallelly and of 45° to the implant axis respectively. Analysis was performed to evaluate the von Mises stress distributions at the peri-implant regions with the help of the Ansys 16 software.Results: The von Mises stresses distributed mostly at the implant cervical regions and the tip ends of the threads on the cortical bone under oblique loading, while on the cancellous bone, the stresses concentrated mostly on the implant lateral cervical regions, the tip ends of the threads and the apical regions. When under vertical loading, the von Mises stresses distributed mostly at the implant cervical regions on the cortical bone while at the tip ends of the threads and the lateral apical regions on the cancellous bone. The von Mises stresses were better distributed on the thread groups under both kinds of loadings compared with no thread design. But there was no obvious difference among the different thread groups. The concentrations of the von Mises stresses on the cancellous bone in the thread groups were mostly at the tip ends of the threads while less in the apical area. The von Mises stresses were better distributed on the cancellous bone on the other three thread designs than on square design.Conclusion: Thread designs are advocated for the reason that adding thread designs to the RAI standard design will have a positive effect on stress distributions at the peri-implant regions and it will reduce the concentrations of von Mises stresses on the cortical bone. From the standpoint of the stress distribution, V-shaped design, buttress design and reverse buttress design are more suitable for RAI than square design. There is no difference of the distributions of the von Mises stresses in the RAI between different thread designs.

Key words: Implant screws, Dental implants, Finite element analysis, Dental stress analysis

中图分类号:

R783.6

林春平,卢松鹤,朱浚鑫,胡洪成,岳兆国,唐志辉. 个性化根形种植体的螺纹形态对周围牙槽骨应力分布影响的三维有限元分析[J]. 北京大学学报（医学版）, 2019, 51(6): 1130-1137.

Chun-ping LIN,Song-he LU,Jun-xin ZHU,Hong-cheng HU,Zhao-guo YUE,Zhi-hui TANG. Influence of thread shapes of custom-made root-analogue implants on stress distribution of peri-implant bone: A three-dimensional finite element analysis[J]. Journal of Peking University(Health Sciences), 2019, 51(6): 1130-1137.

图/表 7

图1

图2

表1

图3

图4

表2

图5

参考文献 37

[1]	Kohal RJ, Hürzeler MB, Mota LF , et al. Custom-made root analogue titanium implants placed into extraction sockets: An experimental study in monkeys[J]. Clin Oral Implants Res, 1997,8(5):386-392.
[2]	Mangano FG, de Franco M, Caprioglio A , et al. Immediate, non-submerged, root-analogue direct laser metal sintering (DLMS) implants: a 1-year prospective study on 15 patients[J]. Lasers Med Sci, 2014,29(4):1321-1328.
[3]	Nair A, Prithviraj DR, Regish KM , et al. Custom milled zirconia implant supporting an ceramic zirconia restoration: a clinical report[J]. KUMU, 2013,11(44):328-331.
[4]	Hodosh M, Povar M, Shklar G , et al. The dental polymer implant concept[J]. J Prosthet Dent, 1969,22(3):371-380.
[5]	Lundgren D, Rylander H, Andersson M , et al. Healing-in of root analogue titanium implants placed in extraction sockets: an experimental study in the beagle dog[J]. Clin Oral Implants Res, 1992,3(3):136-143.
[6]	Pirker W, Kocher A . Immediate, non-submerged, root-analogue zirconia implant in single tooth replacement[J]. Int J Oral Maxillofac Surg, 2008,37(3):293-295.
[7]	Mangano FG, Cirotti B, Sammons RL , et al. Custom-made, root-analogue direct laser metal forming implant: a case report[J]. Lasers Med Sci, 2012,27(6):1241-1245.
[8]	Figliuzzi M, Mangano F, Mangano C . A novel root analogue den-tal implant using CT scan and CAD/CAM: selective laser melting technology[J]. Int J Oral Maxillofac Surg, 2012,41(7):858-862.
[9]	Ivanoff CJ, Grondahl K, Sennerby L , et al. Influence of variations in implant diametes:a 3-to 5-year retrospective clinical report[J]. Int J Oral Maxillofac Implants, 1999,14(2):173-180.
[10]	Hansson S, Werke M . The implant thread as a retention element in cortical bone: the effect of thread size and thread profile: a finite element study[J]. J Biomech, 2003,36(9):1247-1258.
[11]	Huang HL, Chang CH, Hsu JT , et al. Comparison of implant body designs and threaded designs of dental implants: a 3-dimensional finite element analysis[J]. Int J Oral Maxillofac Implants, 2007,22(4):551-562.
[12]	Huang HL, Hsu JT, Fuh LJ , et al. Bone stress and interfacial sliding analysis of implant designs on an immediately loaded maxillary implant: a non-linear finite element study[J]. J Dent, 2008,36(6):409-417.
[13]	Cehreli M, Duyck J, de Cooman M , et al. Implant design and interface force transfer. A photoelastic and strain-gauge analysis[J]. Clin Oral Impl Res, 2004,15(2):249-257.
[14]	梅双, 董福生, 董玉英 , 等. 种植体不同螺纹底部形态对骨界面应力分布的影响[J]. 现代口腔医学杂志, 2016,30(3):138-141.
[15]	Karoussis IK, Bragger U, Salvi GE , et al. Effect of impalnt design on survival and success rates of titanium oral implants: a 10-year prospective cohort study of the ITI Dental Implant System[J]. Clin Oral Implants Res, 2004,15(1):8-17.
[16]	Anssari Moin D, Hassan B, Wismeijer D . A patient specific biomechanical analysis of custom root analogue implant designs on alveolar bone stress: A finite element study[J]. Int J Dent, 2016,8242535. doi: 10.1155/2016/8242535.
[17]	Chen J, Zhang Z, Chen X , et al. Influence of custom-made implant designs on the biomechanical performance for the case of immediate post-extraction placement in the maxillary esthetic zone: a finite element analysis[J]. Comput Methods Biomech Biomed Engin, 2017,20(6):636-644.
[18]	孔亮, 刘宝林, 李德华 , 等. 不同螺纹形态种植体对颌骨应力影响的三维有限元比较研究[J]. 口腔医学研究, 2006,22(2):155-158.
[19]	Tribst JPM, de Morais DC, Alonso AA , et al. Comparative three-dimensional finite element analysis of implant-supported fixed complete arch mandibular prostheses in two materials[J]. J Indian Prosthodont Soc, 2017,17(3):255-260.
[20]	Alvarez-Arenal A, Gonzalez-Gonzalez I, Dellanos-Lanchares H , et al. Influence of implant positions and occlusal forces on peri-implant bone stress in mandibular two-implant overdentures: a 3D finite element analysis[J]. J Oral Implantol, 2017,43(6):419-428.
[21]	Sugiura T, Yamamoto K, Horita S , et al. Effects of implant tilting and the loading direction on the displacement and micromotion of immediately loaded implants: an in vitro experiment and finite element analysis[J]. J Periodontal Implant Sci, 2017,47(4):251-262.
[22]	Yamanishi Y, Yamaguchi S, Imazato S , et al. Influences of implant neck design and implant-abutment joint type on peri-implant bone stress and abutment micromovement: three-dimensional finite element analysis[J]. Dent Mater, 2012,28(11):1126-1133.
[23]	Toniollo MB, Macedo AP, Pupim D , et al. Finite element analysis of bone stress in the posterior mandible using regular and short implants, in the same context, with splinted and nonsplinted prostheses[J]. Int J Oral Maxillofac Implants, 2017,32(4):e199-e206.
[24]	Choi JH, Lee BY, Han JS . Boundary integral method for shape optimization of interface problems and its application to implant design in dentistry[J]. Comput Methods Appl Mech Eng, 2001,190(51-52):6906-6926.
[25]	Mosavar A, Ziaei A, Kadkhodaei M . The effect of implant thread design on stress distribution in anisotropic bone with different osseointegration conditions: a finite element analysis[J]. Int J Oral Maxillofac Implants, 2015,30(6):1317-1326.
[26]	Misch CE . Dental implant prosthetics[M]. St Louis, MO: Mosby, 2005: 322-347.
[27]	Bumgardner JD, Boring JG, Cooper RC Jr , et al. Preliminary evaluation of a new dental implant design in canine models[J]. Implant Dent, 2000,9(3):252-260.
[28]	Steigenga J, Al-Shammari K, Misch C , et al. Effects of implant thread geometry on percentage of osseointegration and resistance to reverse torque in the tibia of rabbits[J]. J Periodontol, 2004,75(9):1233-1241.
[29]	Eraslan O, Inan O . The effect of thread design on stress distribution in a solid screw implant: a 3D finite element analysis[J]. Clin Oral Investig, 2010,14(4):411-416.
[30]	Misch CE . Scientific rationale fordental implant design[M]// Misch CE. Contemporary Implant Dentistry. St. Louis, MO: Elsevier Mosby, 2008: 200-232.
[31]	Javed F, Romanos GE . The role of primary stability for successful immediate loading of dental implants. A literature review[J]. J Dent, 2010,38(8):612-620.
[32]	Baggi L, Di Girolamo M, Vairo G , et al. Comparative evaluation of osseointegrated dental implants based on platform-switching concept: influence of diameter, length, thread shape, and in-bone positioning depth on stress-based performance[J]. Comput Math Methods Med, 2013,250929. doi: 10.1155/2013/250929.
[33]	Oswal MM, Amasi UN, Oswal MS , et al. Influence of three diffe-rent implant thread designs on stress distribution: A three-dimensional finite element analysis[J]. J Indian Prosthodont Soc, 2016,16(4):359-365.
[34]	Ding X, Zhu XH, Liao SH , et al. Implant-bone interface stress distribution in immediately loaded implants of different diameters: a three-dimensional finite element analysis[J]. J Prosthodont, 2009,18(5):393-402.
[35]	Chang PK, Chen YC, Huang CC , et al. Distribution of micromotion in implants and alveolar bone with different thread profiles in immediate loading: a finite element study[J]. Int J Oral Maxillofac Implants, 2012,27(6):e96-101.
[36]	Fuh LJ, Hsu JT, Huang HL , et al. Biomechanical investigation of thread designs and interface conditions of zirconia and titanium dental implants with bone: three-dimensional numeric analysis[J]. Int J Oral Maxillofac Implants, 2013,28(2):e64-71.
[37]	Steigenga JT, al-Shammari KF, Nociti FH , et al. Dental implant design and its relationship to long-term implant success[J]. Implant Dent, 2003,12(4):306-317.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

Materials	Young’s modulus E (GPa)	Poisson’s ratio ν
Titanium	110.00	0.30
Cortical bone	13.70	0.30
Cancellous bone	1.37	0.30
Porcelain	70.00	0.19

Model	M0	M1	M2	M3	M4
Under oblique loading/MPa
Cortical bone	50.9	41.8	37.0	43.4	42.4
Cancellous bone	4.78	17.90	17.00	15.50	14.70
RAI	177.4	151.4	164.3	190.7	170.1
Under vertical loading/MPa
Cortical bone	11.1	11.2	11.7	10.2	10.7
Cancellous bone	1.68	9.03	8.61	7.47	7.40
RAI	33.8	31.3	35.1	34.0	31.2